Мера, интеграл Лебега, гильбертово пространство, страница 7

В различных вопросах, в частности в теории меры, приходится рассматривать суммы и пересечения не только конечного, но и счетного числа множеств. Поэтому целесообразно, помимо понятия кольца множеств, ввести еще следующие понятия.

Определение 3. Кольцо множеств называется -кольцом, если оно вместе с каждой последовательностью множеств  содержит и сумму

Определение 4. Кольцо множеств называется  -кольцом, если оно вместе с каждой последовательностью множеств  содержит пересечение

Естественно назвать  - алгеброй  - кольцо с единицей и  - алгеброй  - кольцо с единицей. Легко, однако, видеть, что эти два понятия совпадают: каждая - алгебра является в то же время - алгеброй, а каждая - алгебра — - алгеброй. Это вытекает из соотношений двойственности:

(см. § 1 гл. 1). - алгебры, или, что то же самое,  - алгебры, называют обычно борелевскими алгебрами, или, короче, В - алгебрами.

Простейшим примером В - алгебры является совокупность всех подмножеств некоторого множества А.

Для В - алгебр имеет место теорема, аналогичная теореме 2, доказанной выше для колец.

Теорема 4. Для любой непустой системы множеств  существует В-алгебра B, содержащая  и содержащаяся в любой алгебре, содержащей .

Доказательство проводится в точности тем же методом, что и доказательство теоремы 2. В -алгебра B называется минимальной В-алгеброй над системой или борелееским замыканием системы .

В анализе важную роль играют так называемые борелевские множества, или. В-множества, которые можно определить как множества на числовой прямой, принадлежащие минимальной В-алгебре над совокупностью всех сегментов [а, b].

В дополнение к сведениям, изложенным в § 7 гл. 1, отметим следующие факты, которые понадобятся нам в гл. VI.

Пусть — функция, определенная на множестве М, со значениями из множества N. Обозначим f(M) систему всех образов f(A) множеств из системы M (предполагается, что M состоит из подмножеств множества М) и  систему всех прообразов множеств из  (предполагается, что состоит из подмножеств множества N). Справедливы следующие утверждения.

1.  Если  есть кольцо, то и  есть кольцо.

2.  Если  есть алгебра, то и  есть алгебра.

3.  Если  есть В-алгебра, то и  есть В-алгебра.

4. 

5.  BB

Пусть  — некоторое кольцо множеств. Если в нем операцию считать «сложением», а «умножением», то  будет кольцом в обычном алгебраическом смысле этого слова. Все его элементы будут удовлетворять условиям:

а + а = 0,    а²   = а.                                                       (*)

Кольца, все элементы которых удовлетворяют условиям (*), называются «булевыми» кольцами. Каждое булево кольцо может быть реализовано как кольцо множеств с операциями  и (Стоун).

§ 35. Меры на полукольцах. Продолжение меры с полукольца на минимальное кольцо над ним

В § 33, рассматривая меру на плоскости, мы отправлялись от меры (площади) прямоугольника и затем распространяли понятие меры на более широкий класс множеств. Как результаты, так и методы, изложенные в § 33, имеют вполне общий характер и могут быть без существенных изменений распространены на меры, определенные на произвольных множествах. Первым шагом в построении меры на плоскости было распространение понятия меры с прямоугольников на элементарные множества, т. е. на конечные суммы попарно непересекающихся прямоугольников.

Абстрактный аналог этой задачи мы рассмотрим в настоящем параграфе.

Определение 1. Функция множества называется мерой, если:

1)  ее область определения  есть полукольцо множеств;

2)  ее значения действительны и неотрицательны;

3)  она аддитивна, т. е. для любого конечного разложения.

множества на множества  выполнено равенство:

Замечание. Из разложения  и 0 вытекает, что , т. е. .

Следующие две теоремы о мерах на полукольцах будут неоднократно использоваться в дальнейшем.

Теорема 1. Пусть — мера, определенная на некотором полукольце . Если множества A₁ ,  ... , А_n,  А принадлежат , причем А_k  попарно не пересекаются и все содержатся в А, то

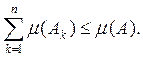
Доказательство. Так как  представляет собой полукольцо, то, согласно лемме 1 § 34, существует разложение S