Другие предметы \ Функциональное программирование

Мера, интеграл Лебега, гильбертово пространство, страница 2

Из можно (по лемме Бореля-Лебега) выбрать конечную систему покрывающую При этом, очевидно,

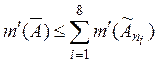
(так как иначе оказалось бы покрытым конечным числом прямоугольников, суммарной площади, меньшей, чем что, очевидно, невозможно). Поэтому

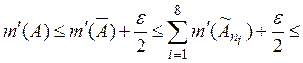
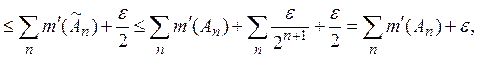
откуда, в силу произвольности вытекает (1).

Совокупность элементарных множеств не исчерпывает всех тех множеств, которые рассматриваются в элементарной геометрии и в классическом анализе. Поэтому естественно поставить вопрос о распространении понятия меры, с сохранением ее основных свойств, на класс множеств, более широкий, чем конечные соединения прямоугольников со сторонами, параллельными осям координат.

Решение этой задачи, в известном смысле окончательное, было дано А. Лебегом в начале XX века.

При изложении лебеговской теории меры нам придется рассматривать не только конечные, но и бесконечные соединения прямоугольников.

Для того чтобы при этом не рассматривать бесконечные значения меры, ограничимся в дальнейшем множествами, целиком принадлежащими квадрату

На совокупности всех таких множеств определим две функция и следующим образом.

Определение 1. Верхней мерой множества А называется число

где нижняя грань берется по всевозможным покрытиям множества А конечными или счетными системами прямоугольников.

Определение 2. Нижней мерой множества А называется число

Легко видеть, что всегда

Действительно, предположим, что для какого-то

т.е.

Тогда, по определению точной нижней грани, можно найти такие системы прямоугольников и покрывающие А и соответственно, что

Объединение систем и обозначим получаем:

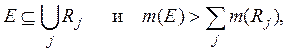
что противоречит теореме 2.

Определение 3. Множество А называется измеримым (в смысле Лебега), если

Общее значение верхней и нижней мер для измеримого множества А называется его лебеговской мерой.

Выясним основные свойства меры Лебега и измеримых множеств. Предварительно установим следующее свойство верхней меры.

Теорема 3. Если

где — конечная или счетная система множеств, то

Доказательство. По определению верхней меры, для каждого найдется такая система прямоугольников конечная или счетная, что и

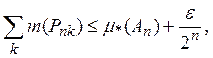
где выбрано произвольно. Тогда

Поскольку произвольно, отсюда вытекает утверждение теоремы.

Выше мы уже ввели понятие меры для множеств, названных нами элементарными. Нижеследующая теорема показывает, что для элементарных множеств определение 3 приводит к тому же самому результату.

Теорема 4. Элементарные множества измеримы, и для них мера Лебега совпадает с построенной выше мерой

Доказательство. Если А — элементарное множество и — составляющие его попарно непересекающиеся прямоугольники, то, по определению,

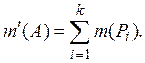
Так как прямоугольники покрывают все А, то Но если — произвольная конечная или счетная система прямоугольников, покрывающая А, то, в силу теоремы 2, поэтому Таким образом,

Так как также является элементарным множеством, то Но

откуда

Следовательно,

Из полученного результата вытекает, что теорема 2 представляет собой частный случай теоремы 3.

Теорема 5. Для измеримости множества А необходимо и достаточно следующее условие: при любом существует такое элементарное множество В, что

Таким образом, измеримыми являются те и только те множества, которые могут быть «с любой степенью точности аппроксимированы» элементарными множествами. Для доказательства теоремы 5 нам понадобится следующая

Лемма. Для любых двух множеств А и В