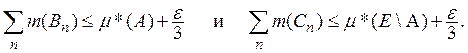
Так как ![]() то
найдется такое N, что
то
найдется такое N, что
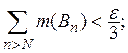
положим
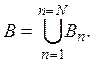
Ясно, что множество
![]()
содержит ![]() а
множество
а
множество
![]()
содержит ![]() и,
следовательно,
и,
следовательно, ![]() При этом
При этом
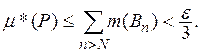
Оценим ![]() Для этого заметим, что
Для этого заметим, что
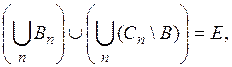
и, следовательно,
![]() (3)
(3)
Но, по условию,
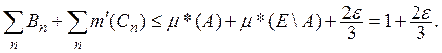 (4)
(4)
Вычитая (3) из (4), получаем:
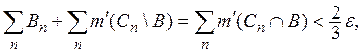
т.е.
![]()
Поэтому
![]()
Итак, если А измеримо, то при любом ![]() существует такое элементарное множество В,
что
существует такое элементарное множество В,
что ![]() Теорема 5 доказана.
Теорема 5 доказана.
Теорема 6. Сумма и пересечение конечного числа измеримых множеств суть измеримые множества.
Доказательство. Достаточно,
очевидно, провести доказательство для двух множеств. Пусть ![]() и
и ![]() — измеримые
множества. Тогда для любого
— измеримые
множества. Тогда для любого ![]() найдутся такие элементарные
множества
найдутся такие элементарные
множества ![]() и
и ![]() что
что
![]()
Так как
![]()
то
![]()
![]()
![]() — элементарное
множество, поэтому, в силу теоремы 4 множество
— элементарное
множество, поэтому, в силу теоремы 4 множество ![]() измеримо.
измеримо.
Но, по самому определению
измеримости, если ![]() измеримо, то и
измеримо, то и ![]() измеримо; поэтому измеримость пересечения
двух измеримых множеств вытекает из соотношения
измеримо; поэтому измеримость пересечения
двух измеримых множеств вытекает из соотношения
![]()
Следствие. Разность и симметрическая разность двух измеримых множеств измеримы.
Это вытекает из теоремы 6 и равенств
![]()
Теорема 7. Если ![]() — попарно непересекающиеся
измеримые множества, то
— попарно непересекающиеся
измеримые множества, то
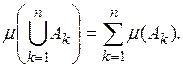
Доказательство. Как и в теореме
6, достаточно рассмотреть случай ![]() Выберем произвольное
Выберем произвольное ![]() и такие элементарные множества
и такие элементарные множества ![]() и
и ![]() что
что
![]() (6)
(6)
![]() (7)
(7)
Положим ![]() и
и ![]() Множество А измеримо в силу теоремы
6. Так как
Множество А измеримо в силу теоремы
6. Так как
![]()
то
![]() (8)
(8)
В силу леммы к теореме 5, из (6) и (7) вытекает, что
![]() (9)
(9)
![]() (10)
(10)
Так как на совокупности элементарных множеств мера аддитивна, то из (8), (9), (10) получаем:
![]()
Заметив еще, что ![]() имеем,
наконец,
имеем,
наконец,
![]()
Так как ![]() может
быть выбрано произвольно малым, то
может
быть выбрано произвольно малым, то
![]()
Поскольку противоположное неравенство
![]()
справедливо всегда при ![]() окончательно
получаем
окончательно
получаем
![]()
так как ![]() и
и ![]() измеримы, то здесь
измеримы, то здесь ![]() можно
заменить на
можно
заменить на ![]() Теорема доказана.
Теорема доказана.
Теорема 8. Сумма и пересечение счетного числа измеримых множеств суть измеримые множества.
Доказательство. Пусть
![]()
— счетная система измеримых множеств, и 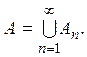 Положим
Положим 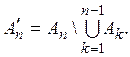 Ясно,
что
Ясно,
что 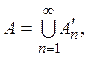 причем множества
причем множества ![]() попарно
не пересекаются. В силу теоремы 6 и следствия из нее все множества
попарно
не пересекаются. В силу теоремы 6 и следствия из нее все множества ![]() измеримы. Согласно теоремам 7 и 3, при
любом конечном п
измеримы. Согласно теоремам 7 и 3, при
любом конечном п
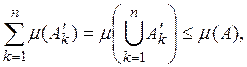
поэтому ряд
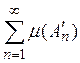
сходится и, следовательно, для любого ![]() найдется такое N, что
найдется такое N, что
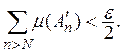 (11)
(11)
Так как множество ![]() измеримо
(как сумма конечного числа измеримых множеств), то для него найдется такое
элементарное множество В, что
измеримо
(как сумма конечного числа измеримых множеств), то для него найдется такое
элементарное множество В, что
![]() (12)
(12)
Поскольку
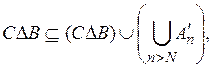
то из (11) и (12) вытекает:
![]()
В силу теоремы 5, отсюда следует измеримость множества А.
Так как дополнения измеримых множеств измеримы, то утверждение теоремы относительно пересечений вытекает из равенства
![]()
Теорема 8 является обобщением теоремы 6. Следующая теорема представляет собой соответствующее обобщение теоремы 7.
Теорема 9. Если ![]() — последовательность
попарно непересекающихся измеримых множеств, и
— последовательность
попарно непересекающихся измеримых множеств, и ![]() то
то
![]()
Доказательство. В силу теоремы 7, при любом N
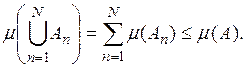
Переходя к пределу при ![]() получаем:
получаем:
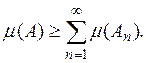 (13)
(13)
С другой стороны, согласно теореме 3,
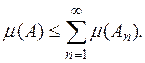 (14)
(14)
Из (13) и (14) вытекает утверждение теоремы.
Установленное в теореме 9
свойство меры называется ее счетной аддитивностью, или ![]() - аддитивностью. Непосредственным
следствием
- аддитивностью. Непосредственным
следствием ![]() - аддитивности является следующее свойство
меры, называемое непрерывностью.
- аддитивности является следующее свойство
меры, называемое непрерывностью.
Теорема 10. Если ![]() — последовательность вложенных друг в друга измеримых
множеств, и
— последовательность вложенных друг в друга измеримых
множеств, и ![]() то
то
![]()
Доказательство. Достаточно,
очевидно, рассмотреть случай ![]() так как общий случай
сводится к этому заменой
так как общий случай
сводится к этому заменой ![]() на
на ![]() Тогда
Тогда
![]()
и
![]()
Следовательно,
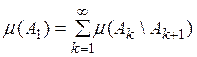 (15)
(15)
и
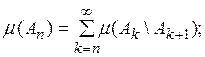 (16)
(16)
так как ряд (15) сходится, то его остаток (16)
стремится к нулю при ![]()
Таким образом,
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.