Мера, интеграл Лебега, гильбертово пространство, страница 11

Пусть на некотором полукольце множеств  с единицей Е задана (- аддитивная мера m. Определим на системе  всех подмножеств множества Е функции и следующим образом.

Определение 1. Верхней мерой множества  называется число

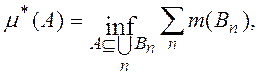
где нижняя грань берется по всем покрытиям множества А конечными или счетными системами множеств .

Определение 2. Нижней мерой множества называется число

Из теоремы 2 §35 вытекает, что всегда

Определение 3. Множество называется измеримым (по Лебегу), если

Если А измеримо, то общее значение мы обозначим и назовем (лебеговской) мерой множества А.

Очевидно, что если А измеримо, то и его дополнение Е \ А тоже измеримо.

Из теоремы 2 § 37 непосредственно вытекает, что для любого - аддитивного продолжения меры т должно выполняться неравенство

Поэтому для измеримого множества А каждое - аддитивное продолжение меры т (если оно вообще существует) необходимо равняется общему значению . Лебеговская мера и есть не что иное, как - аддитивное продолжение меры т на совокупность всех измеримых, в смысле определения 3, множеств.

Определение измеримости можно, очевидно, сформулировать и так:

Определение 3'. Множество называется измеримым, если

Целесообразно наряду с исходной мерой т пользоваться уже известным нам (§35) ее продолжением на кольцо . Ясно, что определению 1 равносильно следующее

Определение 1'.   Верхней мерой множества А называется число

     

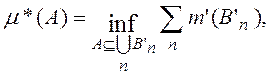
Действительно, так как мера т' - аддитивна (теорема 1 § 37), то любая сумма где  может быть заменена равной ей суммой

         

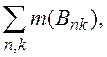
где   если

Основными для дальнейшего являются следующие факты.

Теорема 1. Если

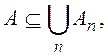
где {А_п}— конечная или счетная система множеств, то

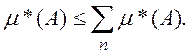
Теорема 2. Если , то  т.е. все множества из измеримы, и для них верхняя и нижняя меры совпадают с т'.

Теорема 3. Для измеримости множества А необходимо и достаточно следующее условие:

при любом  существует такое , что

В § 33 эти утверждения были доказаны для плоской меры Лебега (теоремы 3-5 § 33). Проведенные там доказательства дословно переносятся на рассматриваемый здесь общий случай, поэтому мы их не будем повторять.

Теорема 4. Система M всех измеримых множеств есть кольцо.

Доказательство. Так как всегда

и

то достаточно показать следующее. Если  M и M, то и

M.

Пусть и  измеримы; тогда существуют и такие, что

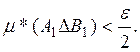
Положив  и воспользовавшись соотношением

получаем:

В силу произвольности  отсюда вытекает измеримость множества А.

Замечание. Очевидно, что Е есть единица кольца M, которое, таким образом, является алгеброй множеств.

Теорема 5. На системе M измеримых множеств функция  аддитивна.

Доказательство этой теоремы представляет собой дословное повторение доказательства теоремы 7 § 33.

Теорема 6. На системе  измеримых множеств функция  - аддитивна.

Доказательство. Пусть

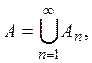
    M,    при

В силу теоремы 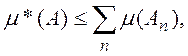1,

                                                    (1)

а в силу теоремы 5, при любом N

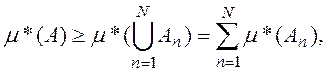
откуда

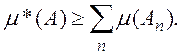                                                      (2)

Из (1) и (2) следует утверждение теоремы.

Итак, мы установили, что функция , определенная на системе M, обладает всеми свойствами - аддитивной меры.

Таким образом, оправдано следующее

Определение 4. Лебеговским продолжением  меры т(А) называется функция , определенная на системе  M измеримых множеств и совпадающая на этой системе с внешней мерой .

В § 33, рассматривая плоскую меру Лебега, мы показали, что не только конечные, но и счетные суммы и пересечения измеримых множеств также являются измеримыми множествами. Это справедливо и в общем случае, т. е. справедлива следующая

Теорема 7. Система M измеримых по Лебегу множеств является борелевской алгеброй с единицей Е.

Доказательство. Так как

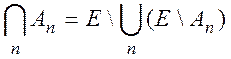
и так как дополнение измеримого множества измеримо, то достаточно показать следующее. Если принадлежат M, то также принадлежит M. Доказательство этого утверждения, проведенное в теореме 8 §33 для плоских множеств, дословно сохраняется и в общем случае.

Так же, как и в случае плоской меры Лебега, из  - аддитивности меры следует ее непрерывность, т. е. если есть  - аддитивная мера, определенная на B-алгебре,  — убывающая цепочка измеримых множеств и