Мера, интеграл Лебега, гильбертово пространство, страница 5

Существование неизмеримых множеств. Выше было показано, что класс измеримых по Лебегу множеств весьма широк. Естественно возникает вопрос о том, существуют ли вообще неизмеримые множества. Покажем, что эта проблема решается положительно. Проще всего неизмеримые множества строятся на окружности.

Пусть С — окружность, длина которой равна 1, и  — некоторое иррациональное число. Отнесем к одному классу те точки окружности С, которые могут быть переведены одна в другую поворотом окружности С на угол (— целое). Каждый из этих классов будет, очевидно, состоять из счетного множества точек. Выберем теперь из каждого такого класса по одной точке. Покажем, что полученное таким образом множество (обозначим его Ф) неизмеримо. Обозначим Ф_n множество, получаемое из Ф с помощью поворота на угол па. Легко видеть, что все множества Ф_n попарно не пересекаются и в сумме составляют всю окружность С. Если бы множество Ф было измеримо, то были бы измеримы и конгруэнтные ему множества Ф_n. Так как

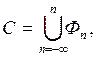
   при

то отсюда следовало бы, в силу —  аддитивности меры

                                                            (17)

Но конгруэнтные множества должны иметь одну и ту же меру:

Отсюда видно, что равенство (17) невозможно, так как сумма ряда, стоящего в правой части равенства (17), равна нулю, если , и равна бесконечности, если . Итак, множество Ф (а следовательно, и каждое Ф_n) неизмеримо.

§ 34. Системы множеств

Изложению общей теории меры мы предпошлем некоторые сведения о системах множеств, дополняющие те элементы теории множеств, которые были изложены в гл. 1.

Системой множеств мы будем называть всякое множество, элементы которого сами представляют собой какие-либо множества. Как правило, мы будем рассматривать системы таких множеств, каждое из которых является подмножеством некоторого фиксированного множества X. Системы множеств мы будем обозначать, как правило, прописными готическими буквами. Основной интерес для нас будут представлять системы множеств, удовлетворяющие, по отношению к введенным в § 1 гл. 1 операциям, некоторым определенным условиям замкнутости.

Определение 1. Кольцом называется непустая система множеств , обладающая тем свойством, что из  и  вытекает принадлежность к  множеств и

Так как для любых А и В

и

то из и  вытекает также принадлежность к  множеств  и. Таким образом, кольцо множеств есть система множеств, инвариантная по отношению к взятию суммы и пересечения, вычитанию и образованию симметричной разности. Очевидно, что кольцо инвариантно и по отношению к образованию любых конечных сумм и пересечений вида

,

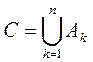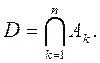
Любое кольцо содержит пустое множество 0, так как всегда Система, состоящая только из пустого множества, представляет собой наименьшее возможное кольцо множеств.

Множество Е называется единицей системы множеств , если оно принадлежит , если для любого  имеет место равенство

Таким образом, единица системы множеств  есть не что иное, как максимальное множество этой системы, содержащее все другие входящие в  множества.

Кольцо множеств с единицей называется алгеброй множеств.

Примеры. 1. Для любого множества А система  всех его подмножеств представляет собой алгебру множеств с единицей .

2.         Для любого непустого множества А система , состоящая из множества А и пустого множества , образует алгебру множеств с единицей

3.         Система всех конечных подмножеств произвольного множества А представляет собой кольцо множеств. Это кольцо будет алгеброй в том и только том случае, когда множество А само конечно.

4.         Система всех ограниченных подмножеств числовой прямой является кольцом множеств, не содержащим единицы.

Из определения кольца множеств непосредственно вытекает

Теорема 1. Пересечение   любого множества колец также является кольцом.

Установим следующий простой, но важный для дальнейшего факт:

Теорема 2. Для любой непустой системы, множеств  существует одно и только одно кольцо , содержащее  и содержащееся в любом кольце , содержащем .