причем множества в правых частях каждого из этих равенств попарно не пересекаются, а суммы по i и j конечны (теорема 3, § 34).
Пусть ![]() Легко
видеть, что множества
Легко
видеть, что множества ![]() попарно не пересекаются, и
притом
попарно не пересекаются, и
притом
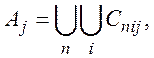
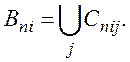
Поэтому, в силу счетной аддитивности меры т на ![]() , имеем:
, имеем:
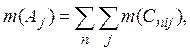 (1)
(1)
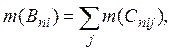 (2)
(2)
а в силу определения меры r(m) на ![]()
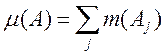 (3)
(3)
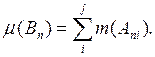 (4)
(4)
Из (1), (2), (3), (4) вытекает, что ![]() (Суммы
по i и по j здесь п
(Суммы
по i и по j здесь п
конечны, ряды по п сходятся.)
Можно было бы показать, что жорданово
продолжение ![]() - аддитивной меры всегда
- аддитивной меры всегда ![]() -аддитивно; нет необходимости делать это
специально, так как это будет вытекать из теории лебеговских расширений,
излагаемой в следующем параграфе.
-аддитивно; нет необходимости делать это
специально, так как это будет вытекать из теории лебеговских расширений,
излагаемой в следующем параграфе.
Докажем
теперь, что для случая ![]() - aддитивных мер теорема 2 §
35 переносится на счетные покрытия:
- aддитивных мер теорема 2 §
35 переносится на счетные покрытия:
Теорема
2. Если мера![]()
![]() -аддитивна и множества А, А1, A2, … , An, …
-аддитивна и множества А, А1, A2, … , An, …
Принадлежат ![]() ,то из
,то из
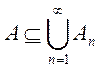
вытекает неравенство
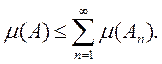
Доказательство. В силу теоремы 1 достаточно провести доказательство для
мер, определенных на кольце, так как из справедливости теоремы 2 для ![]() непосредственно вытекает ее
применимость и к мере m. Если
непосредственно вытекает ее
применимость и к мере m. Если ![]() есть кольцо, то
множества
есть кольцо, то
множества
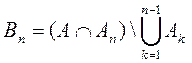
принадлежат ![]() . Так как
. Так как
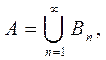
![]()
и множества Вп попарно не пересекаются, то
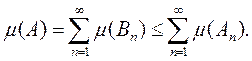
Всюду в дальнейшем мы будем, не оговаривая это особо,
рассматривать только ![]() -аддитивные меры.
-аддитивные меры.
Мы уже рассматривали выше два способа
продолжения мер. По поводу продолжения меры т на кольцо ![]() в § 35 отмечалась единственность этого
продолжения. Аналогично обстоит дело с жордановым продолжением j(m) произвольной меры т. Если множество А измеримо
относительно меры m по Жордану (входит в Sj(m)), то для любой меры
в § 35 отмечалась единственность этого
продолжения. Аналогично обстоит дело с жордановым продолжением j(m) произвольной меры т. Если множество А измеримо
относительно меры m по Жордану (входит в Sj(m)), то для любой меры ![]() ,
продолжающей т и определенной на А, значение
,
продолжающей т и определенной на А, значение ![]() совпадает со значением J(A) жорданова продолжения J = j(m). Можно показать, что
продолжение меры т за пределы системы Sj(m) не будет однозначно. Более точно это значит следующее.
Назовем множество А множеством однозначности для меры т, если:
совпадает со значением J(A) жорданова продолжения J = j(m). Можно показать, что
продолжение меры т за пределы системы Sj(m) не будет однозначно. Более точно это значит следующее.
Назовем множество А множеством однозначности для меры т, если:
1) существует мера, являющаяся продолжением меры m, определенная для множества А;
2) для любых двух такого рода мер ![]() и
и ![]()
![]() .
.
Имеет место теорема: система множеств однозначности для
меры т совпадает с системой множеств, измеримых по Жордану относительно
меры т, т. е. с системой множеств ![]() .
.
Однако, если рассматривать только ![]() - аддитивные меры и их продолжения (
- аддитивные меры и их продолжения (![]() -аддитивные), то система множеств
однозначности будет, вообще говоря, обширнее.
-аддитивные), то система множеств
однозначности будет, вообще говоря, обширнее.
Так как именно случай ![]() -
аддитивных мер нас будет занимать далее, то установим
-
аддитивных мер нас будет занимать далее, то установим
Определение 2. Множество А называется множеством ![]() - однозначности для (
- однозначности для (![]() -аддитивной
-аддитивной ![]() , если
, если
1) существует ![]() - аддитивное
продолжение
- аддитивное
продолжение ![]() меры т, определенное для А (т.
е. такое, что
меры т, определенное для А (т.
е. такое, что ![]() );
);
2) для двух таких ![]() -
аддитивных продолжений
-
аддитивных продолжений ![]() и
и ![]() справедливо
равенство:
справедливо
равенство:
![]()
Если А есть множество ![]() -
однозначности для
-
однозначности для ![]() - аддитивной меры
- аддитивной меры ![]() , то, в силу нашего определения, существует
единственно возможное
, то, в силу нашего определения, существует
единственно возможное ![]() для
для ![]() - аддитивного продолжения меры
- аддитивного продолжения меры ![]() , определенного на А.
, определенного на А.
Хотя жорданово продолжение позволяет распространить
понятие меры на довольно широкий класс множеств, оно во многих случаях
оказывается все же недостаточным. Так, например, если мы в качестве исходной
меры возьмем площадь, за область ее определения примем полукольцо
прямоугольников и будем рассматривать жорданово продолжение этой меры, то уже
такое сравнительно простое множество, как множество точек, координаты которых
рациональны и удовлетворяют условию ![]() , не будет измеримо по
Жордану.
, не будет измеримо по
Жордану.
Распространение
![]() - аддитивной меры, определенной на
некотором полукольце на класс множеств, в известном смысле максимальный, может
быть получено с помощью так называемого лебеговского продолжения. В этом
параграфе мы рассмотрим лебеговское продолжение меры, заданной на полукольце с
единицей. Общий случай будет рассмотрен в § 39.
- аддитивной меры, определенной на
некотором полукольце на класс множеств, в известном смысле максимальный, может
быть получено с помощью так называемого лебеговского продолжения. В этом
параграфе мы рассмотрим лебеговское продолжение меры, заданной на полукольце с
единицей. Общий случай будет рассмотрен в § 39.
Проводимое ниже построение представляет собой, в значительной мере, повторение в абстрактных терминах построения меры Лебега для плоских множеств, проведенное в § 33.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.