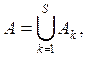
![]()
![]()
в котором первые п множеств совпадают с заданными множествами А1 , …. , An. Так как мера любого множества неотрицательна, то
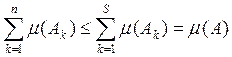
Теорема 2.
Если А1 , …. , An, А
принадлежат ![]() , и
, и 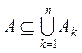 , то
, то
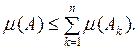
Доказательство.
Согласно лемме 2 § 34, найдется такая система
попарно непересекающихся множеств B1 , …. , Bt из ![]() , что каждое из множеств A, А1
, …. , Anпредставляется как
соединение некоторых из множеств Вs:
, что каждое из множеств A, А1
, …. , Anпредставляется как
соединение некоторых из множеств Вs:
![]() ;
; ![]() ; k = 1,2, … ,
n.
; k = 1,2, … ,
n.
При этом каждый индекс ![]() принадлежит
и какому-либо из
принадлежит
и какому-либо из ![]() . Следовательно, каждый член
суммы
. Следовательно, каждый член
суммы
![]()
входит один или несколько раз в двойную сумму
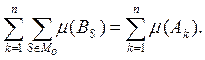
Отсюда и вытекает, что
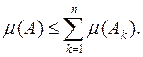
В частности, при п = 1 получаем
Следствие. Если ![]() , то
, то ![]()
Определение 2. Мера ![]() называется продолжением меры
т(А), если
называется продолжением меры
т(А), если ![]() , и для каждого
, и для каждого ![]() имеет место равенство
имеет место равенство
![]()
Основной целью настоящего параграфа является доказательство следующего предложения.
Теорема 3. Каждая мера т(А) имеет одно и только одно продолжение![]() , имеющее своей областью
определения кольцо
, имеющее своей областью
определения кольцо ![]() .
.
Доказательство. Для каждого множества ![]() существует
разложение
существует
разложение
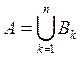
![]() (1)
(1)
(теорема 3,§ 34). Положим, по определению,
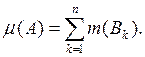 (2)
(2)
Легко видеть, что величина ![]() , определенная
равенством (2), не зависит от выбора разложения (1). Действительно, рассмотрим
два разложения
, определенная
равенством (2), не зависит от выбора разложения (1). Действительно, рассмотрим
два разложения
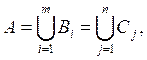
![]()
![]()
Так как все пересечения ![]() принадлежат
принадлежат
![]() , то, по аддитивности меры m,
, то, по аддитивности меры m,
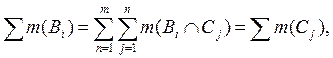
что и требовалось доказать. Неотрицательность и
аддитивность функции ![]() , определяемой равенством
(2), очевидны. Итак, существование продолжения
, определяемой равенством
(2), очевидны. Итак, существование продолжения ![]() меры m доказано.
Для доказательства его единственности заметим, что, по определению продолжения,
если
меры m доказано.
Для доказательства его единственности заметим, что, по определению продолжения,
если 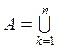 , где Bk — непересекающиеся
множества из Sm, то для любого
продолжения
, где Bk — непересекающиеся
множества из Sm, то для любого
продолжения ![]() меры m на кольцо
меры m на кольцо ![]()
![]()
т.е. мера ![]() совпадает с мерой
совпадает с мерой ![]() , определенной равенством (2). Теорема
доказана.
, определенной равенством (2). Теорема
доказана.
Связь этой теоремы с построениями § 33 будет вполне ясна, если заметить, что совокупность прямоугольников на плоскости представляет собой полукольцо, площадь этих прямоугольников является мерой в смысле определения 1, а элементарные плоские множества образуют минимальное кольцо над полукольцом прямоугольников.
В этом параграфе мы рассмотрим в общей форме тот процесс, который в случае плоских фигур позволяет от определения площадей для конечных соединений прямоугольников со сторонами, параллельными осям координат, перейти к площадям всех тех фигур, которым приписывает определенную площадь элементарная геометрия или классический анализ. С полной отчетливостью этот переход был проведен французским математиком Жорданом около 1880 г. Основная идея Жордана восходит, впрочем, еще к математикам древней Греции и состоит в приближении, измеряемого множества А множествами А' и А", которым мера уже приписана, изнутри и снаружи, т. е. таким образом, чтобы выполнялись включения
![]()
Так как любую меру мы умеем продолжать на кольцо (теорема 3
§ 35), то естественно предполагать исходную меру m определенной на кольце ![]() . Такое допущение будет
принято на протяжении всего данного параграфа.
. Такое допущение будет
принято на протяжении всего данного параграфа.
Определение 1. Будем называть множество А измеримым по Жордану,
если при любом ![]() в кольце
в кольце ![]() имеются
множества А' и A", удовлетворяющие условиям
имеются
множества А' и A", удовлетворяющие условиям
![]()
![]()
Теорема 1. Система ![]() измеримых по Жордану
множеств является кольцом.
измеримых по Жордану
множеств является кольцом.
Действительно, пусть ![]() ,
,
![]() ; тогда при любом
; тогда при любом ![]() существуют
А', А", В', В"
существуют
А', А", В', В" ![]() такие, что
такие, что
![]()
и
 ,
, 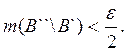
Отсюда
![]() (1)
(1)
![]() (2)
(2)
Так как
![]()
то
![]()
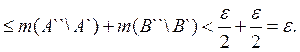 (3)
(3)
Так как
![]()
то
![]()
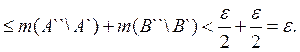 (4)
(4)
Поскольку ![]() произвольно, а
множества
произвольно, а
множества ![]() принадлежат
принадлежат ![]() ,
то из (1), (2), (3), (4) вытекает, что
,
то из (1), (2), (3), (4) вытекает, что ![]() и
и ![]() принадлежат
принадлежат ![]() .
.
Пусть M—
система таких множеств А, для которых существует множество ![]() из
из ![]() . Для
любого A из M
положим по определению
. Для
любого A из M
положим по определению

Функции ![]() и
и ![]() называются, соответственно, «внешней» и
«внутренней» мерой множества А. Очевидно, что всегда
называются, соответственно, «внешней» и
«внутренней» мерой множества А. Очевидно, что всегда
![]()
Теорема 2. Кольцо![]() совпадает с системой тех множеств
совпадает с системой тех множеств ![]() M, для которых
M, для которых ![]()
Доказательство. Если
![]()
то
![]()
и для любых А' и А" из ![]() , таких, что
, таких, что ![]()
![]()
![]()
![]()
т. е. А не может входить в ![]() .
.
Обратно, если
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.