доказательство.
Легко видеть, что кольцо ![]() определяется системой
определяется системой ![]() однозначно.
Для доказательства его существования рассмотрим соединение
однозначно.
Для доказательства его существования рассмотрим соединение ![]() всех множеств А, входящих в
всех множеств А, входящих в ![]() и кольцо M(X) всех подмножеств множества X. Пусть
и кольцо M(X) всех подмножеств множества X. Пусть ![]() — совокупность всех
колец множеств, содержащихся в M (Х) и содержащих
— совокупность всех
колец множеств, содержащихся в M (Х) и содержащих ![]() . Пересечение
. Пересечение
B = ![]()
всех этих колец и будет, очевидно, искомым кольцом ![]() .
.
Действительно, каково бы ни было кольцо ![]() , содержащее
, содержащее ![]() ,
пересечение
,
пересечение ![]() M (Х) будет
кольцом из
M (Х) будет
кольцом из ![]() и, следовательно,
и, следовательно,
![]() B
B![]()
т. е. B действительно удовлетворяет
требованию минимальности. ![]() называется
минимальным кольцом над системой
называется
минимальным кольцом над системой ![]() .
.
Фактическое
построение кольца ![]() по
исходной системе
по
исходной системе ![]() , вообще говоря, довольно
сложно. Оно становится, однако, вполне обозримым в том важном частном случае,
когда система
, вообще говоря, довольно
сложно. Оно становится, однако, вполне обозримым в том важном частном случае,
когда система ![]() является «полукольцом».
является «полукольцом».
Определение 2. Система множеств ![]() называется полукольцом, если она
содержит пустое множество
называется полукольцом, если она
содержит пустое множество ![]() , замкнута по отношению
к образованию пересечений и обладает тем свойством, что из принадлежности к
, замкнута по отношению
к образованию пересечений и обладает тем свойством, что из принадлежности к ![]() множеств А и
множеств А и ![]() вытекает возможность представления А
в виде
вытекает возможность представления А
в виде 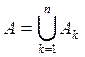 , где Ak — попарно непересекающиеся множества из
, где Ak — попарно непересекающиеся множества из ![]() , первое из которых есть заданное
множество А1.
, первое из которых есть заданное
множество А1.
В дальнейшем всякую систему попарно непересекающихся множеств A1,A2,…An, соединение которых есть заданное множество, мы будем называть конечным разложением множества А.
Всякое кольцо множеств ![]() является
полукольцом, так как если А и
является
полукольцом, так как если А и ![]() входят в
входят в ![]() , то имеет место разложение
, то имеет место разложение
![]() , где
, где ![]() .
.
Примером полукольца, не являющегося кольцом множеств, может служить совокупность всех интервалов (а, b), сегментов [а, b] и полусегментов [а, b) и (а, b] на числовой прямой[1].
Для того чтобы выяснить, каким образом строится кольцо множеств, минимальное над данным полукольцом, установим некоторые свойства полуколец множеств.
Лемма 3. Пусть множества A1,A2,…An,,A принадлежат
полукольцу![]() , причем
множества Аi попарно не пересекаются и все являются подмножествами
множества А. Тогда множества Ai(i = 1,2,..., n) можно
включить в качестве первых п членов в конечное разложение
, причем
множества Аi попарно не пересекаются и все являются подмножествами
множества А. Тогда множества Ai(i = 1,2,..., n) можно
включить в качестве первых п членов в конечное разложение
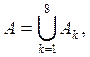
![]()
множества А, причем все.
доказательство проведем по индукции. При п = 1 справедливость утверждения леммы вытекает из определения полукольца. Предположим, что это утверждение справедливо для n = m и рассмотрим т + 1 множеств A1 ,…, A m , A m+1, удовлетворяющих условиям леммы. По сделанному предположению,
![]()
где все множества ![]() (q = 1,2,… p) принадлежат
(q = 1,2,… p) принадлежат ![]() . Положим
. Положим
![]()
По определению полукольца, имеется разложение
![]()
где все ![]() принадлежат
принадлежат ![]() . Легко видеть, что
. Легко видеть, что
![]()
Таким образом, утверждение леммы доказано для n = m + 1, а следовательно, и вообще для всех п.
Лемма 4. Какова бы ни была конечная система множеств Ai ,..., Ап,
принадлежащих полукольцу ![]() , найдется в
, найдется в ![]() такая конечная система попарно
непересекающихся множеств B1 ,..., At,
что каждое Ak может
быть представлено в виде суммы
такая конечная система попарно
непересекающихся множеств B1 ,..., At,
что каждое Ak может
быть представлено в виде суммы
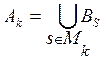
некоторых из множеств Bs.
Доказательство. При n = 1 лемма
тривиальна, так как достаточно положить t = 1, В1 =A1. Допустим, что она справедлива для n = m и рассмотрим в ![]() некоторую систему
множеств А1 ... Am+1. Пусть B1, B2 ,..., Bt — множества из
некоторую систему
множеств А1 ... Am+1. Пусть B1, B2 ,..., Bt — множества из ![]() , удовлетворяющие условиям леммы по отношению
к A1, A2, …,Ат. Положим
, удовлетворяющие условиям леммы по отношению
к A1, A2, …,Ат. Положим
![]()
В силу леммы 1, имеет место разложение:
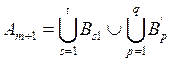 ,
, ![]() (1)
(1)
а в силу самого определения полукольца имеет место разложение
![]() ,
, ![]() .
.
Легко видеть, что

![]()
и что множества
![]()
попарно не пересекаются. Таким образом, множества ![]() удовлетворяют
условиям леммы по отношению к A1 … Am, Am+1. Лемма доказана.
удовлетворяют
условиям леммы по отношению к A1 … Am, Am+1. Лемма доказана.
Теорема 3. Если —![]() полукольцо, то
полукольцо, то ![]() совпадает
с системой Z множеств А,
допускающих конечные разложения
совпадает
с системой Z множеств А,
допускающих конечные разложения
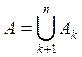
на множества ![]()
Доказательство. Покажем, что система Z образует кольцо. Если А и В — два произвольных множества из Z, то имеют место разложения
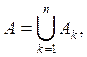
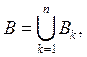
![]()
![]()
Так как ![]() — полукольцо, то
множества
— полукольцо, то
множества
![]()
тоже входят в ![]() . В силу леммы 1 имеют
место разложения
. В силу леммы 1 имеют
место разложения
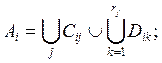
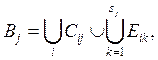 (2)
(2)
где ![]() Из
равенств (2) вытекает, что множества
Из
равенств (2) вытекает, что множества ![]() и
и ![]() допускают разложения
допускают разложения
![]()
и, следовательно, входят в Z - Таким образом, Z действительно представляет собой кольцо; его минимальность среди всех колец, содержащих в, очевидна.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.