Министерство образования и науки Российской Федерации
Федеральное агентство по образованию
Государственное образовательное учреждение
высшего профессионального образования
«Комсомольский-на-Амуре государственный технический университет»
Расчётно-графическое задание.
по дисциплине «Функциональный анализ»
Студент группы 4ВС-1 Рогозин В.А.
Преподаватель: Хусаинов А.А.
Комсомольск-на-Амуре
2006
Ответить на следующие вопросы:
(a) Является ли метрическим пространством заданное множество M с определенной на нем функцией d: M´M ® M ?
(b) Будет ли (M, d) полным метрическим пространством?
M – множество замкнутых отрезков [x,y] на прямой, d([x1,y1], [x2 ,y2 ] ) = | x1 – x2| + |y1 – y2|
Решение:
(a)Для того чтобы множество было метрическим пространством, необходимо чтобы выполнялись следующие аксиомы:
Проверим выполнение каждой из этих аксиом для данного множества.
1) |x1-x2|+|y1-y2| >= 0 очевидно, т.к. |x1-x2| и |y1-y2| >= 0 (выполняется)
2) d(|x1,y1|,|x2,y2|) = |x1-x2|+|y1-y2| = |x2-x1|+|y2-y1| = d(|x2,y2|,|x1,y1|) (выполняется)
3) d(|x1,y1|,|x2,y2|) + d(|x2,y2|,|x3,y3|) >= d(|x1,y1|,|x3,y3|);
|x1-x2|+|y1-y2| + |x2-x3|+|y2-y3| >= |x1-x3|+|y1-y3|
Пусть у1 и х1 будет левой точкой, а х3 и у3 – правой, тогда x1>x2>x3 и у1>y2>y3. Тогда x1-x2+y1-y2+x2-x3+y2-y3 >= x1-x3+y1-y3
x1-x3+y1-y3 >= x1-x3+y1-y3
0 >= 0 (неравенство верно, значить 3-я аксиома выполняется)
Так как выполняются все аксиомы, то исходное множество является метрическим пространством.
(c) M - множество замкнутых отрезков [x,y] на прямой,
d(|x1,y1|,|x2,y2|) = |x1-x2|+|y1-y2|
Рассмотрим в этом пространстве последовательность попарно не пересекающихся отрезков:
[xn,yn] = [n,n-1/(2^n)], тогда для любых m.n > N существует Nɛ d([xm,ym],[xn,yn]) < ½m+ ½n < 2/2Nɛ < ɛ
|xm – yn| < ɛ -фундаментальная последовательность
|ym - yn| < ɛ(xn,yn) –фундаментальная последовательность
x=lim xn y=lim yn
[x,y]=lim[xn,yn] => существует n : [xn,yn] < [x,y]
Но для такой последовательности любой отрезок, концы которого совпадают будет является пределом, следовательно данная последовательность не будет иметь предела, значит не является фундаментальной. Отсюда следует, что исходное пространство является полным.
Построить оператор для решения заданного уравнения. Доказать, что он является сжимающим. Построить последовательные решения интегрального уравнения и оценить точность
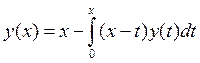 , y0(x)=0. y(x)=sin x
, y0(x)=0. y(x)=sin x
Решение:
Доказать, что топология метрического пространства удовлетворяет аксиоме отделимости Хаусдорфа.
x1,x2 є (M,d), если x1 ≠ x2 => существует ɛ > B(x1, ɛ) ∩ B(x2, ɛ) = 0
Решение:
ɛ = d(x1,x2)/4
пусть x є B(x1, ɛ) ∩ B(x2, ɛ), тогда d(x1,x2) < d(x,x2) + d(x,x2) < 2ɛ = d(x1,x2)/2 =>
d(x1,x2) = 0, что противоречит условию => топология метрического пространства удовлетворяет аксиоме отделимости Хаусдорфа, что и требовалось доказать.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.