Бесстолкновительные явления при наличии пространственного заряда, страница 9

легко численно рассчитать универсальную кривую распределения потенциала как функцию координаты в безразмерных переменных. Определим безразмерный потенциал

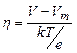                                                                                        (2.58)

где  V_m — минумум потенциала,     Т — температура    эмиттера, а также безразмерную длину

ξ = 2β(x—x_m),(2.59)

где

β²= (2/π/9) (J/χ) (kT/e)^-3/2,                                                                (2.60)

а параметр Чайлда χ = (4ε₀/9) определяется из уравнения (2.9б). Ниже покажем, что связь между этими переменными задаётся выражением[3]

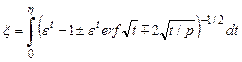                                                         (2.61а,б)

где функция 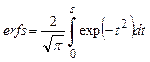                                                                                                          (2.62)

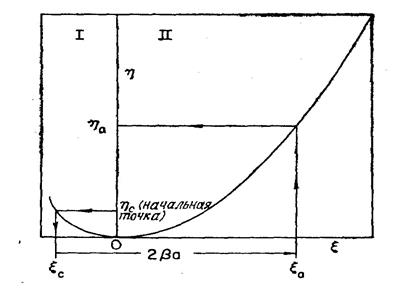
— табулированный интеграл ошибок. Верхние арифметические знаки в уравнении (2.61 а, б) относятся к области I на рис. 2.12, т. е. к области между катодом и минимумом потенциала, а нижние—к области II. Эти выражения можно проинтегрировать численно и получить кривую типа показанной на рис. 2.13, которую можно использовать для нахождения вольт-амперных характеристик следующим образом.

В случае плоского диода с заданными расстоянием а, температурой катода Т и работой выхода φ используем формулу Ричардсона

J_s = AT²exp(-eφ/kT)                                                                         (2.63)

для нахождения плотности тока эмиссии J_s. (Эта формула детально рассмотрена, например, в работе [146].) Выберем любую плотность тока J, меньшую, чем J_s. В случае максвеллов-ского распределения ток через единичную площадку при наличии тормозящего потенциала V_rзадается выражением

J = J_sexp(-eV_r/kT).                                                                    (2.64)

Для эмитированных электронов     высота     потенциального барьера равна V_c— V_m, так что

J/J_s = ехр(— η_с),                                                              (2.65)

где η_с = e(V_c—V_m)/kT. Тогда начальные условия для J_s и J имеют вид

                                                                                                  (2-66)

Зная η_с и ход кривой η(ξ) в области I, легко определить ξ_с. Из (2.60) найдем β, а из (2.59) —безразмерное расстояние между катодом и анодом:

ξ_a— ξ_с = 2βа,                                                                     (2.67)

здесь a — расстояние между анодом и катодом. Прибавив это расстояние к ξ_с, получим (см. рис. 2.13) безразмерную координату анода ξ_a. Затем найдем соответствующее значение η_а нормированного потенциала анода. Тогда искомая разность потенциалов между анодом и катодом равна

                                                                    (2.68)

Указанную процедуру вычислений можно повторить для любых J < J_s и получить вольт-амперную кривую J(V).

Полезно отметить, что kT/e=1В при T =11600 К. Значит, если потенциал выражен в вольтах, то kT/e можно заменить на (T / 11 600).

Для получения соотношений (2.61 а) и (2.616) необходимо выделить эмитируемые электроны со скоростью υ₀ в направлении х и затем проинтегрировать по υ₀. В случае плоского диода нас не интересуют поперечные компоненты скорости и под кинетической энергией будем понимать кинетическую энергию продольного (вдоль х) движения. Ток, переносимый частицами с начальной кинетической энергией в диапазоне от eV₀до e(V₀+dV₀), соответствует уменьшению тока, обусловленному возрастанием тормозящего потенциала от V₀до V₀+dV₀. Из (2.64) получим уравнение

dJ = (J_se/kT) exp {- еV₀ / kT) dV₀.                                                        (2.69)

Поскольку

еV₀= тυ²₀/2                                                                                         (2.70)

е dV₀=тυ₀dυ₀,                                                                                (2.71)

уравнение (2.69) примет вид

dJ = (J_smυ₀/kT) exp (— mυ²₀/2kT) dυ₀.                                                    (2.72)