Бесстолкновительные явления при наличии пространственного заряда, страница 13

                                                ΔV/V=J/18J                                                                                                                     (2.106)

где

J₀= χ  V^3/2 /a²                                                                                                                      (2.107)

при

χ = (4ε₀/9)(2е/М)^1/2                                                                                                               (2.108)

есть плотность тока Чайлда, который, согласно уравнениям (2.9а) и (2.9б), можно пропустить сквозь промежуток, равный ширине пучка. Как можно видеть, вплоть до значений J порядка Jо предположение ΔV<< Vвполне корректно.

Поскольку вне пучка поле Е_х постоянно, легко определить падение потенциала ΔV'  между пучком и эквипотенциальной граничной поверхностью

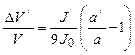                                                                          (2.108)

где а' — ширина канала, в котором движется длинный ленточный пучок. Сделанный выше вывод о том, что торможением пучка можно пренебречь вплоть до J~J_о, справедлив, если ширина канала превосходит ширину пучка не более чем вдвое.

Если предположить, что потенциал в пучке тот же, при котором он инжектируется, так ч|то справедливо уравнение (2.104), то получим ускорение еЕх/М иона на кромке пучка, положив х = а/2. Это дает

d²x/dt² = (Ja/2ε₀) (e/2M)^1/2V ^-1/2.                                                          (2. 1 10)

Поскольку J может изменяться поперек пучка и наверняка уменьшается по мере его расширения, предпочтительно заменить J на ток I = Jab, тогда получим

d²x/dt²= (I/2bε₀) (e/2M)^1/2V ^-1/2.                                                            (2.111)

Ускорение на кромке при расширении пучка остается постоянным, так что легко вычислить x(t) для иона, стартующего при х = а/2 и z = 0. В результате находим

х = (а/2) + (I/4bε₀) (e/2MV)^1/2 t ²                                                                                  (2. 112)

Время t исключается, если  использовать соотношение z == υt при υ =.

Получим           

х/a=(l/2) + (I/18I₀) (z/а)²                                                                                           (2.113)

где ток   I₀=J_oab определяется как

                                                    I₀χ  V^3/2 /(b/а)                                                                                   (2.114)

Поскольку пространственный заряд пропорционален I/V^3/2, его воздействие обычно описывается величиной

Р = I/V^3/2                                                                                            (2.115)

называемой первеансом. Однако воздействие пространственного заряда связано не только с первеансом, но и с массой иона. Первеанс ионного пучка часто характеризуется эквивалентным первеансом электронного пучка, получаемого при умножении Р на Необходимо отметить, что в формуле (2.115) отсутствует геометрический    фактор b/а и она имеет тот недостаток, что определяет   размерную величину;    следует помнить,    что 2,334 эквивалентного электронного    микропервеанса  (где микропервеанс равен  10^-6 А/В^3/2)   соответствуют очень сильному влиянию пространственного заряда в ионных пучках с b/a = 1. Иногда, используют аспектное отношение, т. е. квадрат отношения ширины апертуры,    при которой    извлекаются    ионы, к расстоянию между ускоряющим и плазменным электродами на рис. 1.1. Для электродных систем, в которых длина ускорения не превышает более чем втрое ширину щели, эта величина не имеет смысла вследствие различных эффектов. К ним относятся: провисание эквипотенциальных поверхностей и влияние отношения ускоряющего и замедляющего напряжений, так что величина I/I₀, описывающая,    согласно     (2.113), расширение, обусловленное действием пространственного заряда, не определяется исключительно    аспектным    отношением. В действительности величина I/I₀, которую можно назвать эквивалентным аспектным отношением, является наилучшим рабочим параметром, и мы назовем ее нормированным первеансом П. Определение П = I/I₀, где I₀ задается уравнением  (2.114), приводит к соотношению