Следует решить уравнение (2.4), но с начальными условиями
V = V0, V' =0 при x= 0, (2.38)
где V0 = mυ20/2e.Введем удобные для решения задачи единицы. Используем безразмерный потенциал
η = V/V0, (2.39)
и безразмерную координату
ξ = x/x0, (2.40)
где
х0= (2/3) ![]() (2e/m)1/4V03/4
(2.41а)
(2e/m)1/4V03/4
(2.41а)
или х0=![]() V03/4
(2.41б)
V03/4
(2.41б)
есть длина ускорения Чайлда, соответствующая данным J и V0. Константа χ определена соотношением (2.9б). В переменных η и ξ уравнение (2.4) имеет вид
η" = (4/9)η-1/2 (2.42)
с начальными условиями
η' = 0, η = 1 при ξ = 0. (2.43)
Штрихи у η означают дифференцирование по ξ. Первое интегрирование с учетом начальных условий дает выражение
(η')2 = (16/9)(![]() -1).
(2.44)
-1).
(2.44)
Тогда можно записать
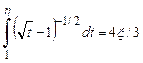 (2.45)
(2.45)
Интеграл легко вычисляется, если ввести новую переменную
интегрирования (![]() — 1)1/2,
и мы получим
— 1)1/2,
и мы получим
(![]() -1)1/2(
-1)1/2(![]() +2) = ξ
(2.46)
+2) = ξ
(2.46)
или, используя выражения (2.39), (2.40) и (2.41), имеем
(![]() — 1) 1/2(
— 1) 1/2(![]() +2) V03/4= (3x/2) (m/2e)1/4 (J/ε0)1/2 .
(2.47)
+2) V03/4= (3x/2) (m/2e)1/4 (J/ε0)1/2 .
(2.47)
Легко заметить, что при ![]() >> l это
уравнение совпадает с (2.7) и, следовательно, с уравнением Чайлда (2.9).
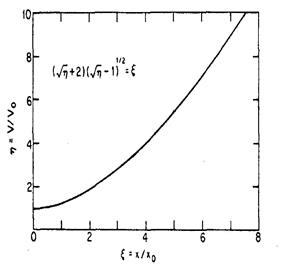
Уравнение (2.47) нельзя ,решить относительно V, но можно для заданных значений J, V0 и е/т построить график V(x) или, исходя из (2.46),
построить универсальный график η(ξ) (рис. 2.4).
>> l это
уравнение совпадает с (2.7) и, следовательно, с уравнением Чайлда (2.9).
Уравнение (2.47) нельзя ,решить относительно V, но можно для заданных значений J, V0 и е/т построить график V(x) или, исходя из (2.46),
построить универсальный график η(ξ) (рис. 2.4).
Полезно разрешить уравнение (2.47) относительно толщины слояа— расстояния, на котором потенциал доходит до определенной величины V, и сравнить это расстояние с толщиной слоя, полученной при решении уравнения Чайлда относительно х,
|
записав
a/a1 = (![]() -1)1/2(
-1)1/2(![]() +2)η-3/4,(2.48)
+2)η-3/4,(2.48)
где а1 — толщина слоя Чайлда, вычисленная для той же величины V потенциала коллектора. Чтобы рассчитать относительную толщину слоя для того же падения потенциала в слое, необходимо найти толщину слоя Чайлда a2 для напряжения V— V0. Тогда получим
a/a2 = (![]() -1)1/2(
-1)1/2(![]() +2)(η-1)-3/4. (2.49)
+2)(η-1)-3/4. (2.49)
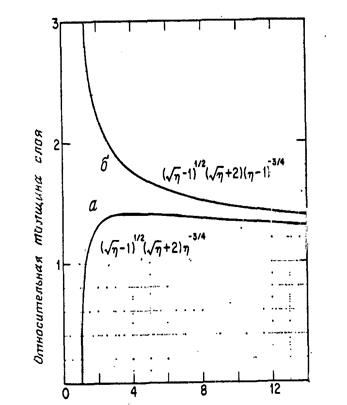
Относительная толщина слоя как функция ηпредставлена на рис. 2.5 [кривые а (2.48) и б (2.49)]. Как можно видеть, абсолютная толщина заметно возрастает с начальной энергией ионов даже при не слишком больших значениях V/V0. Полезно отметить, что выражение
![]() (2.50)
(2.50)
хорошо аппроксимирует (2.49) при η > 2 и может быть использовано вместо (2.48) при η > 8 с точностью, достаточной для большинства приложений.
В проведенном анализе были рассмотрены электроны или ионы, которые, согласно рис. 2.1, двигались слева направо, т.е. удалялись от поверхности с нулевым градиентом потенциала. Ситуация полностью аналогична и в случае ионов, движущихся по-другому, а именно, замедляющихся в направлении к границе с нулевым градиентом потенциала. Один из двух слоев, рассмотренных в задаче 2.8, — тормозящий слой, удовлетворяющий этому условию.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.