Бесстолкновительные явления при наличии пространственного заряда, страница 4

Пространственный заряд обычно не играет существенной роли в ионных пучках релятивистских энергий, поскольку переносимая таким пучком мощность должна быть чрезвычайно большой, но для анализа электронного потока могут потребоваться релятивистские поправки. Во всяком случае релятивистское обобщение проводится с помощью метода, изложенного в разд. 2.5, настолько просто, что не требуется дополнительных аргументов в пользу того, чтобы) выполнить эту процедуру. Вместо импульса mυ в релятивистском случае следует использовать

р = mυ[1 — υ²/c²] ^-1/²,                                                                  (2.28)

где скорость υ в плоскости коллектора получается приравниванием кинетической энергии уменьшению потенциальной энергии:                               

mc²([1 — υ²/c²] ^-1/2-1) =  eV.                                                                 (2.29)

Это приводит к выражению

   [1 — υ²/c²] ^-1/2 = 1 + ( eV/mc²),                                                           (2.30)

из которого получим

                         υ = (2 eV/m)^1/2[1 + ( eV/2mc²) ] ^1/2  [1 + ( eV/mc²) ] ^-1.                                                          (2.31)

Умножим импульс частицы, задаваемый формулами (2.28), (2.30) и (2.31), на поток частиц через единичную площадку (J/e) и приравняем это электростатическому натяжению на коллекторе для того, чтобы удовлетворить закон сохранения импульса (разд. 2.5). Тогда получим уравнение

 (Jm/e)(2 eV/m)^1/2[1 + ( eV/2mc²) ] ^1/2  = ε₀V '²/2.                                           (2.32)

Разрешив уравнение (2.32) относительно производной Vи разделив переменные, имеем

V^-1/4[1 + ( eV/2mc²) ]^{- 1/4} dV= 2 (J/ε₀)^1/2 (т/2е)^1/4 dx.                                                          (2.33)

Обозначим eV/2mc² через s, тогда можно записать

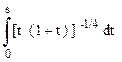 =  2 (J/ε₀)^1/2 (т/2е)^1/4 (e/2mc²)^3/4x. .                                                  (2.34)

Хотя в общем виде данное уравнение не решается, однако, предположив, что s мало, можно представить подынтегральное выражение в виде t ^-1/4  [ 1 - t / 4 ] и получить

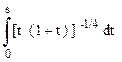≈ s^3/4(1 -s + ...)                                                              (2.35)

Если   отбросить члены   высших степеней   по s,   то (2.34) и (2.23) дают

J =[(4ε₀ / 9) V^3/2/x²][1 -  (eV/mc²)  ].                                                 (2.36)

Это выражение переходит    в  (2.8)  при eV/mc²<<1. Точное решение уравнения (2.34) можно записать в виде

                 J/J₀ = (9/16)s^-3/2[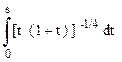]²                                                                                           (2.37)

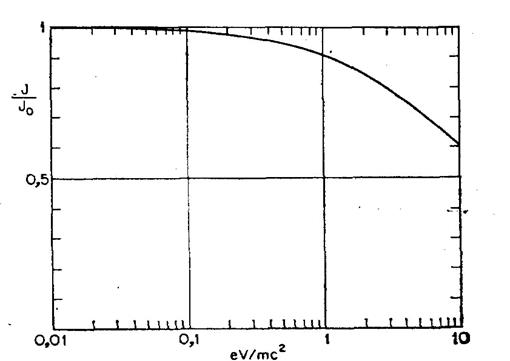
где J₀ — ток Чайлда, определяемый формулой (2.8). Результаты численного интегрирования вплоть до значений 2s= = eV/mc² = 10 показаны на рис. 2.3. Эти результаты эквивалентны уравнениям, полученным, исходя из уравнения Пуассона, в работе [148].

	Рис.2.3. Отношение тока, ограниченного пространственным зарядом, к току, полученному из нерелятивистского уравнения Чайлда

 

2.7. Слой при ненулевых начальных скоростях

Рассмотрим теперь поток между двумя параллельными плоскостями при наличии пространственного заряда при том же условии dV/dx = 0 на эмиттере, но будем считать, что все эмитированные частицы имеют начальную скорость υ₀в направлении, перпендикулярном поверхности эмиттера. Этот случай входит в круг задач, учитывающих пространственный заряд и рассматриваемых в разд. 2.8, но представляет особый интерес, и проще рассмотреть его отдельно. Вначале задача может показаться надуманной, искусственной, поскольку здесь нет ограничения по току, как в задаче Чайлда. А именно, частицы, имеющие начальную энергию, могут двигаться к коллектору, несмотря на наличие тормозящего поля вблизи эмиттера. Условие V' = 0 на границе при наличии направленной скорости у инжектированных частиц возникает тогда, когда электрод находится под потенциалом, отрицательным относительно плазмы. Плазма становится эмиттером положительных ионов, имеющих энергию направленного движения,  и положительно заряженное пространство между плазмой, где V' ≈ 0, и электродом обычно называют просто слоем. Реальные слои более сложны, нежели те, которые рассмотрены в данном разделе в идеализированной постановке задачи, поскольку ионы имеют разброс по скоростям, а электроны движутся сквозь слой наружу вплоть до потенциалов порядка kT_e /e. Тем не менее введенный здесь термин «слой» — это пространство между двумя эквипотенциальными  поверхностями, когда на одной из них напряженность электрического поля должна быть почти нулевой. Это определение включает область между двумя плоскостями при удовлетворении граничных условий Чайлда (2.5).