Бесстолкновительные явления при наличии пространственного заряда, страница 2

Следует отметить, что плотность заряда ρ, задаваемая формулой (2.2), и, следовательно, V"(х) обращаются в бесконечность на поверхности эмиттера. Это не представляет затруднений, поскольку бесконечность интегрируема, но с методологической точки зрения может вызвать неудобство. В реальной ситуации бесконечности нет, так как существует разброс частиц по скоростям. В разд. 2.7 будет показано, насколько хорошо полученное решение аппроксимирует решение в реальной ситуации.

2.3. Коаксиальные цилиндры

Прежде чем написать уравнение, аналогичное уравнению (2.8) для коаксиальных цилиндров и концентрических сфер (см. разд. 2.4), полезно отметить, что ограниченный пространственным зарядом электронный ток между эмиттером с нулевым потенциалом и анодом с потенциалом V_a всегда удовлетворяет условию

I ~ V_a^3/2,                                                                              (2.10)

как было показано Ленгмюром (1913 г.). Это следует из таких рассуждений. Потенциал V в каждой точке должен быть пропорционален потенциалу V_a коллектора, если нормальная компонента градиента потенциала на эмиттере остается равной нулю. Тогда, согласно уравнению Пуассона (1.1), в каждой точке

                      ρ ~ V_a                                                                                                                    (2.11)

Поскольку скорость частицы в соответствие с (2.3) пропорциональна, для каждой точки справедливо соотношение

              υ  ~ V_a^1/2.                                                                             (2.12)

Тогда плотность тока в каждой точке равна

J = ρυ ~ V_a^3/2,                                                                        (2.13)

и, следовательно, полный ток с учетом ограничения пространственным зарядом удовлетворяет условию (2.10) для двух-электродной задачи любой геометрии.

В случае коаксиальных цилиндров V является функцией только расстояния r от оси, и уравнение Пуассона можно записать в виде

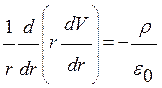                                                                                             (2.14)

В этом случае ρ задается выражением

ρ = —i/2πrυ,(2.15)

где i — электронный ток на единицу длины, а υ — скорость, удовлетворяющая соотношению (2.3). Комбинируя (2.14), (2.15) и (2.3), получим выражение

rd²V/dr² + dV/dr = (i/2πε₀).(2.16)

Решение этого уравнения в замкнутой форме не найдено, но Ленгмюр (1913 г.) представил решение в виде

i =(8 πε₀/9)  V^3/2/rβ²                                                                                                     (2.17)

где β² — функция отношения радиуса r крадиусу эмиттера r₀. Используя константу χ из формулы (2.9б), можно записать следующее выражение:

i = 2πχV ^3/2/rβ².                                                                          (2.18)

Ленгмюр и Блоджетт [175] подставили выражение (2.17) в уравнение (2.16) и получили функцию β в виде ряда. Некоторые табулированные ими величины приведены в табл. 2.1. Величины β² для сходящегося потока ( r < r₀) табулированы как (-β²).

Уравнение (2.17) сразу решается относительно V, и для любого заданного значения i и радиуса эмиттера r₀ сразу находят V(r), как это показано в решении задачи 2.5.

2.4. Концентрические сферы

Легко построить физические ситуации, когда имеем поток, ограниченный влиянием пространственного заряда, между плоскими параллельными электродами, расстояние между которыми настолько мало по сравнению с их размерами, что применимо приближение бесконечных плоскостей. Цилиндрические эмиттер и коллектор встречаются очень часто, например эмитирующая нить на оси цилиндрического коллектора. Но не очевидно, что ограниченный пространственным зарядом поток между концентрическими сферами интересен для эксперимента, поскольку имеются трудности создания электрического контакта с внутренней сферой. Однако, в разд. 5.3 будет показано, что можно оперировать коническим сектором сферической геометрии, сохраняющим свойство, присущее концентрическим сферам, т.е. зависимость потенциала только от радиуса. Кроме того, поле в слое вокруг сферического зонда под отрицательным потенциалом, находящегося в плазме, подчиняется исследуемым в данном разделе уравнениям в предельном случае, когда начальные скорости ионов малы по сравнению со скоростью, вычисленной по падению потенциала в слое.