Бесстолкновительные явления при наличии пространственного заряда

Глава 2

БЕССТОЛКНОВИТЕЛЬНЫЕ ЯВЛЕНИЯ ПРИ НАЛИЧИИ ПРОСТРАНСТВЕННОГО ЗАРЯДА

2.1.         Краткое содержание

Явления, связанные с влиянием пространственного заряда, ассоциируются с потоком заряженных частиц, количество которых достаточно для того, чтобы их плотность существенно изменяла потенциал той области, через которую проходят частицы. В данной главе рассматриваются потоки ионов и электронов различной геометрической конфигурации, но в каждом случае движение частицы определяется исключительно электростатическим полем, создаваемым электродами и коллективным воздействием других заряженных частиц. Обсуждение влияния парных столкновений или других процессов, ведущих к установлению равновесия, будет проведено в последующих разделах книги.

Типичной бесстолкновительной задачей, представляющей интерес для разработки ионных источников, в которой необходим учет влияния пространственного заряда, является определение геометрии электродов и величины потенциалов. Эти потенциалы следует приложить к электродам для того, чтобы извлечь ионы из плазмы, ускорить их до требуемой энергии при минимальном взаимодействии с электродами и выпустить в виде пучка с малой угловой расходимостью. Чтобы представить проблему во всей ее полноте, необходимо сформулировать и решить последовательность частных задач нарастающей сложности. Полезно начать с анализа потока заряженных частиц между бесконечными параллельными плоскостями.

2.2.         Плоские параллельные электроды (уравнение Чайлда)[1]

Рассмотрим поток заряженных частиц между двумя параллельными плоскостями, например поток электронов от плоского катода к плоскому аноду. Идеализируем задачу, предположив, что плоскости бесконечны, и частицы эмитируются с нулевой скоростью. Для определенности будем полагать, что заряженные частицы есть электроны[2] с зарядом q = - е. Результаты будут  пригодны для ионов, если изменить знак потенциала. Эта задача была решена Чайлдом в 1911 г. [49] и позднее переработана Ленгмюром [169].

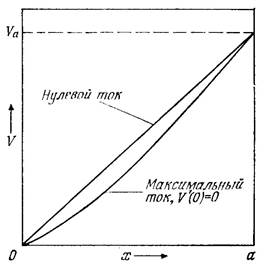Картина распределения потенциала между эмиттером (х=0) при нулевом потенциале и коллектором (х = а)под потенциалом V_a показана на рис. 2.1. По мере увеличения тока пучка пространственный заряд вызывает провисание кривой V(x) до тех пор, пока электрическое поле не обратится в нуль при х = 0. Для частиц, эмитируемых с нулевой скоростью, это соответствует максимальному току, и такое решение представляет особый интерес.

В одномерном случае уравнение Пуассона  (1.1)  имеет вид

                    V"(х) = — ρ/ε₀.                                         (2.1)

Через V"(х) обозначена производная d²V/dx². В уравнении (2.1) можно положить

                             ρ =— J /υ,                                            (2.2)

где J — плотность тока, υ —cкорость частицы. Поскольку поток — однонаправленный и стационарный, J не зависит от х, а скорость υ задается выражением

                                      υ= (2eV/m)^1/2                                                                                         (2.3)

Подставив (2.2)   и (2.3) в (2.1), получим

V"(x) = (J/ε₀)(m/2eV)^1/2.                                                 (2.4)

Это уравнение следует решить с начальными условиями

V' = 0    и    V = 0    при    х = 0.                                                        (2.5)

Первое интегрирование уравнения (2.4), которое можно упростить, умножив левую часть на 2V'dx, а правую на эквивалентную величину 2dV, приводит к выраженю

                                   (V')² = 4(J/ε₀)(mV/2e)^1/2                                                                                                       (2.6)

Константу интегрирования следует положить равной нулю в соответствии с (2.5). Переменные V и х в (2.6) легко разделяются; при втором интегрировании получим выражение

V = (т /2е)^{1 /3} ( J/ε₀) ^2/3 ( З х /2) ^{4 / 3}                                                                                                                                                                         (2.7)

Константа интегрирования, согласно (2.5), и на этот раз равнa нулю. Поскольку V=V_a при х=а, имеем

J = (4ε₀ / 9) V_a^3/2/а²,                                                                                (2.8)

т.е. хорошо известное уравнение Чайлда в системе единиц СИ. Удобно записать это уравнение, используя константу χ в виде

J= χV_a ^3/2/а²                                                                                                                                                                           (2.9а)

где

χ = (4ε₀/9) (2е/т)^1/2                                                                                                                                        (2.9б)

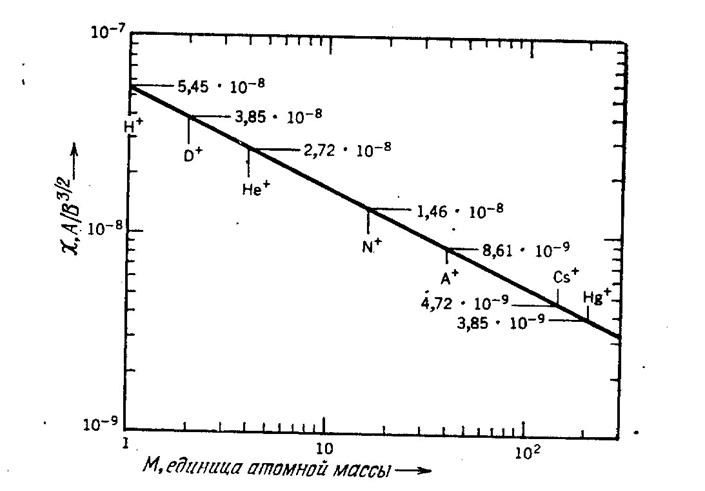Для электронов эта константа равна 2,334ּ10^-6 А/В^3/2, ее величина для однократно заряженных ионов как функция атомной массы показана на рис. 2.2. Полезно указать, что в уравнении Чайлда расстояние а удобнее выражать в сантиметpax, а не в метрах; при этом плотность тока J берется в амперах, деленных на квадратный сантиметр.