Бесстолкновительные явления при наличии пространственного заряда, страница 11

Падение потенциала V_c— V_mне может быть слишком большим по сравнению с kT/e, так что утверждения, что η велико и V>>V_mпочти эквивалентны. Далее, утверждение V>>V_m подразумевает, что х>>х_т, так что для больших η можно написать

J = J₀(1 + 2,66/),                                                                 (2.93)

где J₀ — плотность тока в уравнении Чайлда. Несомненно, что J →J₀ при η→∞, и это действительно оправдывает использование уравнения Чайлда, но неверно утверждение, согласно которому η должно быть бесконечно большим, если уравнение Чайлда считается точным. Например, если η = 500, то плотность тока, предсказываемая уравнением (2.93), на 12% выше J₀. При температуре катода 2320 К величина kT/e = 0,2 В и значение η = 500 соответствует напряжению 100 В.

Другое указание на масштаб ошибки, возникающей при использовании уравнения Чайлда, следует из рис. 2.14. В переменных (η, ξ), используемых в данном разделе, уравнение Чайлда записывается в виде

η=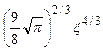.                                                                    (2.94)

Эта зависимость изображена  штриховой линией.

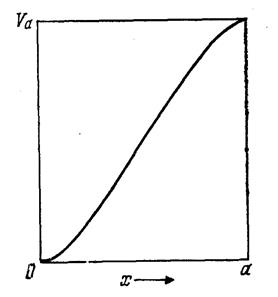
2.10. Двойной слой при нулевых начальных скоростях

Рассмотренные до сих пор задачи, связанные с пространственным зарядом, были униполярными, т. е. были связаны с заряженными частицами одного сорта. Если же эмиттер электронов с ограничением по пространственному заряду поддерживается под отрицательным потенциалом относительно плазмы, возникает слой, в котором ионы плазмы ускоряются в направлении эмиттера, а электроны из эмиттера — в направлении плазмы. Как показано на рис. 2.15, в этом случае кривая потенциала должна иметь нулевой наклон на левом конце из-за ограниченного пространственным зарядом потока эмитированных электронов с нулевой начальной скоростью и нулевой наклон на правом конце для сшивки с полем в плазме. Такой слой называется двойным, поскольку в одной половине

(слева) преобладает влияние пространственного заряда электронов, а в другой — пространственного заряда ионов. Решим вначале идеализированную задачу, полагая, что и ионы, и электроны эмитируются с нулевой скоростью двумя фиксированными плоскостями с разностью потенциалов V_aмежду ними. Ленгмюр [172] рассмотрел эту задачу, решая уравнение Пуассона. Можно устранить одно интегрирование, если использовать закон сохранения импульса (разд. 2.3), как это сделал Форрестер [93]. Отметим, что можно рассматривать любую плоскость между х=0 и х=а в качестве источника ионов, но для того, чтобы воспроизвести ситуацию точно, следует при этом считать, что ионы имеют скорость, где V— потенциал плоскости, а М — масса иона. Конечно, такие ионы порождают силу отдачи. Полное уравнение сохранения импульса можно получить, приравняв силу на катоде силе на плоскости

                                                 (2.95)

где последний член в правой части описывает электростатическую силу, действующую на плоскость, эмитирующую ионы. Положив V=V_aи V'=0, получим

J_i/J_e =                                                                     (2.96)

Исключив J_i из   (2.95)   путем подстановки (2.96) и положив η=V/V_a , ξ = х/а, можно записать

η' ² = (16/9) (J_e/J₀) (- 1 +),                                                   (2.97)

Где                                    J=[(4ε₀ / 9) V_а^3/2/а²]                                                                                   (2.98)

есть ток Чайлда, соответствующий напряжению V_aи зазору а. Поскольку η = 0 при ξ = 0, из (2.97) получим соотношение

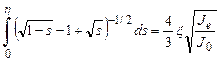                                                              (2.99)

Из условия η = 1 при ξ = 1 имеем

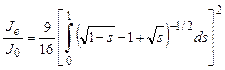                                                       (2.100)

43

Численный расчет интеграла приводит к выражению

J_e/J₀= 1,8651[4].                                                                  (2.101)

Из структуры интеграла в (2.99) можно видеть, что потенциал симметричен относительно срединной плоскости. Из этой симметрии следует, что поток ионов будет больше потока Чайлда в 1,8651 раза. Квадратный корень из этого числа дает