Бесстолкновительные явления при наличии пространственного заряда, страница 15

который в табличной форме приведен, например, в книге [3]. Интеграл в левой части (2.128) есть (r₀/r)F

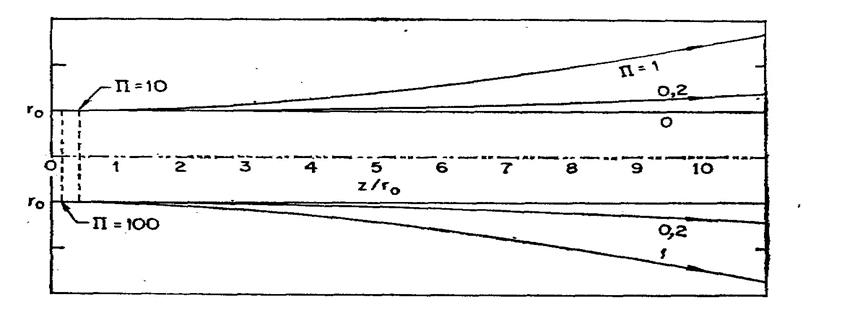
Расширение пучка, полученное расчетным путем, показано на рис. 2.17 для двух значений нормированного первеанса. Его легко получить для любых П из кривой при П=1, умножая координату zна множитель П^-1/2.

В следующем ниже разделе будет показано, что Смит и Гартман [256] решили эту задачу в общем случае, когда учитывалось замедление ионов вследствие изменения потенциала.

В. Сильноточные пучки

Хотя из выражений (2.106) и (2.121) следует, что изменение потенциала в ионном пучке при единичном нормированном первеансе мало, оказывается невозможным пропустить пучки с П>>1 без нейтрализации пространственного заряда пучка. По мере нарастания тока возрастающий внутри пучка потенциал вызывает увеличение пространственного заряда, что приводит к большему, чем следует из выражения (2.128), расширению пучка. Однако быстрое увеличение плотности пространственного заряда при возрастании тока должно фактически вызвать остановку и отражение пучка. Это происходит скачкообразно, подобно тому, как описано в разд. 2.8. А именно, потенциал непрерывно спадает по мере роста тока инжекции до тех пор, пока не достигнет критического минимума, большего нуля: Любое дальнейшее увеличение тока инжекции приведет к отражению ионов и уменьшению пропускаемого тока.

Расстояние z₀ до плоскости отражения задается уравнением Чайлда при плотности тока 2J и напряжении V

z₀ = (2/3) (ε₀/2J)¹'² (2е/М)^1/4 V³'⁴.                                                                 (2. 1 30)

Для ленточных пучков выражение примет вид

z₀/а = (J₀/2J)^1/2,                                                                         (2.131)

где Jо определяется из (2.98), а — ширина пучка. С использованием нормированного первеанса имеем

z₀/а = (2П)^-1/².                                                                          (2.132)

На рис. 2.16 показана длина торможения для двух значений П. Для пучков круглого сечения положим J=I/πr₀² в (2.129). Затем подставим I/χV^3/2 = Пи получим выражение

z₀/r₀=(π/2П)^1/2                                                                                                       (2.133)

для длины торможения, показанной на рис. 2.17 при П = 10 и 100.

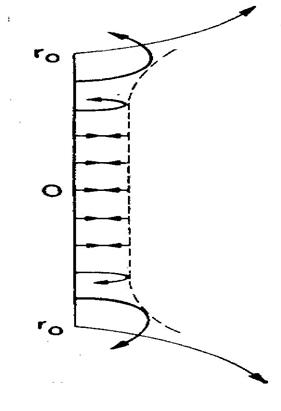
Поверхность отражения видна на рис. 2.16 как плоскость. Если расстояние до этой поверхности мало по сравнению с диаметром пучка, можно ожидать, что для центральной части пучка она плоская. Однако скорее всего вблизи кромки потенциал будет менее положительным, чем в центре, и отражающая ионы поверхность, а также ионные траектории будут такими, как показано на рис. 2.18.

Переходная область между малыми нормированными первеансами, когда потенциал в пучке почти не изменяется под влиянием пространственного заряда, и случаем, когда возникает отражение, была изучена в работе [256]. Содержание указанной работы здесь приводить не будем, но некоторые факты являются интересным добавлением к нашему рассмотрению. В случае, когда цилиндрический пучок с нормированным первеансом 1 находится в камере, диаметр которой в десять раз больше диаметра пучка, пучок расширяется до радиуса, составляющего 0,91 расстояния, показанного на рис. 2.16 для П=1. В этом случае уравнение (2.102) дает падение потенциала между пучком и стенкой камеры, равное 16,3 % напряжения V. Интересно, что поправка настолько мала, что, согласно проведенной ранее оценке, можно использовать рис. 2.17 для значений П вплоть до единицы.

С описанными в данном разделе явлениями расширения или остановки пучка можно справиться посредством нейтрализации пространственного заряда частицами противоположного знака. Действительно, трудно избежать появления захваченных медленных ионов в электронном пучке или медленных электронов в ионном пучке. Эти захваченные частицы уменьшают глубину ямы и поэтому поперечные поля влияют на частицы в пучке. Расширение ионного пучка с компенсированным пространственным зарядом обсуждается в гл. 6.