Бесстолкновительные явления при наличии пространственного заряда, страница 3

Таблица 2.1. Геометрические параметры для течения с ограничением пространственным зарядом между цилиндрами и сферами

 

	Указание:r0 — радиус эмиттера, r — радиус коллектора; параметры β2 и α2 соответствуют расходящемуся потоку, т.е. r>r0; (—β2) и (—α2) — сходящемуся потоку, т.е. r<r0.

 

Общим для случаев параллельных плоскостей, коаксиальных цилиндров и концентрических сфер является то, что силовые линии электрического поля и траектории заряженных частиц прямолинейны и совпадают друг с другом. В случае концентрических сфер уравнение Пуассона можно записать в виде

.                                                                 (2.19)

где ρ задается выражением

ρ = —I/4πr²υ,                                                                          (2.20)

a υ, как и выше, удовлетворяет   формуле  (2.3). Комбинация выражений приводит к уравнению

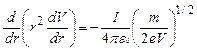                                                      .                                                        (2.21)

Как и в случае коаксиальных цилиндров, решение этого уравнения в замкнутой форме не найдено, но Ленгмюр я Блоджетт [176] представили решение в виде

I = (16πε₀ / 9) V^3/2/α²                                                                                              (2.22)

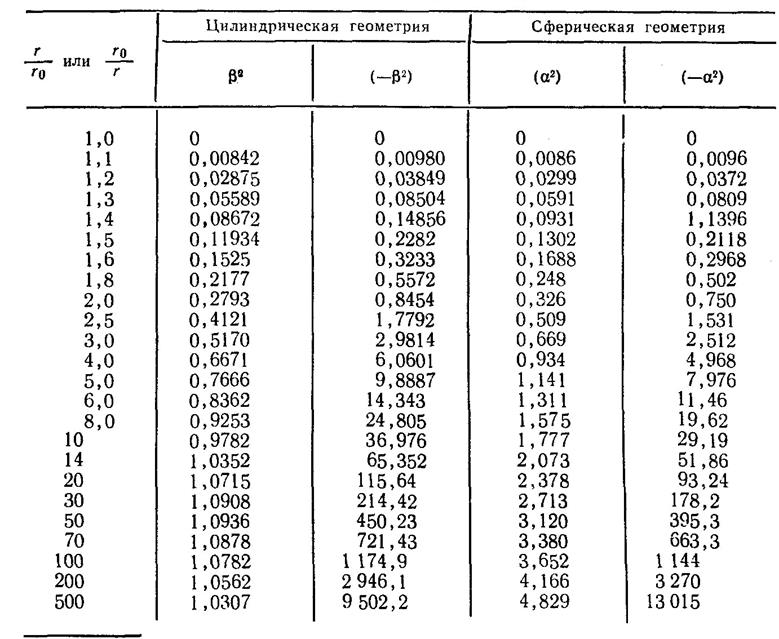
где параметр α2 определялся либо в виде ряда, либо в виде интеграла при подстановке (2.22) в уравнение (2.20). Некоторые табулированные значения α2 приведены в табл. 2.1. Уравнение (2.22) можно записать в форме

I =4πχV ^3/2/α²                                                                                                                                             (2.23)

Для заданногоr₀параметр α² есть функция r, следовательно, при заданном I выражение (2.23) определяет потенциал V как функцию r.

Полезно сравнить плотность тока эмиттера для трех рассматриваемых нами типов геометрии. В плоско-параллельном случае имеем         

J = χV ^3/2/x²                                                                                                                                  (2.24)

В случае цилиндрической геометрии  J = i/2πr₀и соответственно

J = χV ^3/2/r₀rβ²;                                                                                 (2.25)

при сферической геометрии J  = I/4πr₀², что приводит к выражению

J = χV ^3/2/r²₀α².                                                                                  (2.26)

2.5. Метод баланса импульса

Интересно то, что уравнение Чайлда можно получить другим способом, описанным Форрестером в 1981 г. [93]. Этот способ не предполагает использования уравнения Пуассона и проще в том смысле, что устраняет одно интегрирование.1) Хотя и нет необходимости выводить заново уравнение Чайлда, продемонстрируем этот способ на данном примере в качестве инструмента, полезного при решении других задач, в том числе плазменных.

Потенциал V(x), удовлетворяющий условиюV'(0)=0, представлен нижней кривой на рис. 2.1. Замена коллектора при х = а другим электродом под потенциалом V(x) при меньших х не меняет распределения потенциала в области от нуля до х. При любом местонахождении коллектора суммарная сила, действующая на эмиттер и коллектор, должна быть равна нулю вследствие сохранения импульса. В нашем частном случае, когда электроны испускаются с нулевой скоростью в нулевом электрическом поле (V ' = 0), сила, действующая на эмиттер, отсутствует. Таким образом, потребуем, чтобы суммарная сила на коллектор была равна нулю. Приравнивая передачу импульса заряженными частицами на единицу площади коллектора электрическому натяжению ε₀(V ')²/2, получим

 (J/e)m(2eV/m)^1/2 = ε₀V '²/2.                                                               (2.27)

Как нетрудно заметить, полученное соотношение эквивалентно (2.6), и, следовательно, приводит к уравнению Чайлда (2.8).

2.6. Релятивистское уравнение Чайлда