Бесстолкновительные явления при наличии пространственного заряда, страница 10

В области между катодом и минимумом потенциала (область I на рис. 2.12) имеются электроны, движущиеся в обоих направлениях +х и —х. Проще рассмотреть область II, где имеются только электроны с положительными скоростями, что мы и сделаем.

Каждый элементарный ток дает вклад в пространственный заряд

dρ = — dJ/υ,                                                                           (2.73)

где υ есть x-компонента скорости в произвольной точке х. Полный пространственный заряд получим, интегрируя по всем электронам, которые преодолевают потенциальный барьер в точке х_m. Это дает выражение

ρ = - (mJ_s/kT) 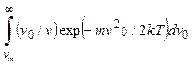,                                                       (2.74)

где

.                                                                   (2.75)

Скорость υ выражается через υ₀ и потенциал V следующим образом:                  

                                          1/2 тυ²=  1/2 тυ²₀  + e(V-V_c).                                                                (2.76)

В данной точке V фиксировано, и

тυdυ =тυ₀dυ₀.                                                                           (2.77)

Используя (2.76) и (2.77) для замены переменной интегрирования υ₀ на υ, получим

ρ = - (mJ_s/kT)exp[e(V-V_c)/kT] 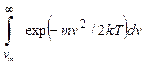 ,                                      (2.78)

где

                  (2.79)

Плотность тока на анод равна

J = J_s ехр {— e(V-V_c)/kT},                                                                    (2.80)

так что (2.78) можно записать в виде

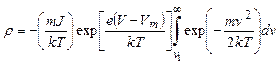.                                                            (2.81)

Положив mυ²/2kT = s², получим

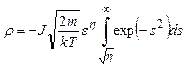                                                                           (2.82)

где η — безразмерный потенциал, определенный согласно (2.58). Поскольку d²η/dx² = (e/kT)d²V/dx², уравнение Пуассона будет иметь вид

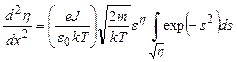                                                                 (2.83)

Интеграл от до бесконечности есть разность между интегралом от нуля до бесконечности и интегралом от нуля до. Так как интеграл от ехр( — s²) в пределах (0,) есть /2, получим

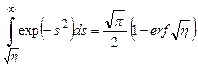                                                                              (2.84)

где функция erf определена согласно (2.62). Используя выражения (2.59) и (2.60) и подставляя в уравнение (2.83) ξ вместо х, приведем его к более простому виду

η" = 1/2ε^η(1 — erf),                                              (2.85)

Следует решить это уравнение с условиями η = 0 и η'=0 при ξ = 0. Уравнение (2.85) можно проинтегрировать тем же способом, что и уравнение (2.41); это дает

(η')² = 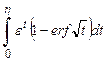                                                           (2.86)

или

 (η')² = 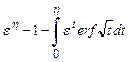                                                  (2.87)

После интегрирования по частям получим

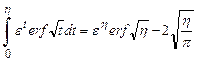                                                                (2.88)

Подставим это в  (2.87), извлечем квадратный  корень из правой и левой частей и проинтегрируем; в результате придем к уравнению (2.61б), т. е. искомое решение находится в области II.

В области I (рис. 2.12) полезно разделить ρ на две части: часть а, обусловленную электронами, движущимися к аноду, и часть б, связанную с электронами, движущимися к катоду. Часть а формируется электронами, для которых выполняется условие

e(V_c — V)< 1/2тυ²₀< ∞,                           (2.89)

а часть б обусловлена электронами при соблюдении неравенства

e(V_c — V)<1/2тυ²₀<e(V_c — V_m).              (2.90)

Предлагаем читателю в качестве упражнения выполнить вычисления,  аналогичные тем, которые были  сделаны для области II (или посмотреть публикацию Ленгмюра [170]), и показать, что в области I уравнение

η=         (2.91)

заменяет уравнение (2.85) и что его решение приводит к уравнению (2.61 а).

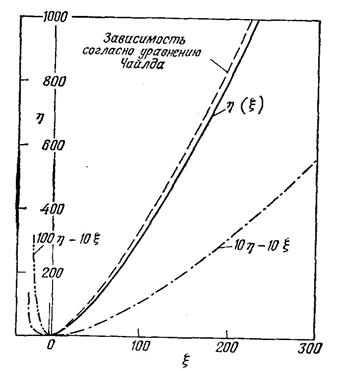
Искомый график η(ξ), который можно использовать так же, как график на рис. 2.13, представлен на рис. 2.14.

Для больших ηи ξ >0 Ленгмюр нашел представление ξ(η) в виде ряда. Учет первых двух членов ряда приводит к зависимости:

J= (4ε₀/9) (V— V_m)^3/2 (x—x_m)^-2(1 + 2,66η^-1/2).                                             (2.92)