Бесстолкновительные явления при наличии пространственного заряда, страница 7

Все случаи проанализированы и опубликованы [238, 85], однако результаты слишком обширны для того, чтобы приводить их здесь полностью. Обычно кривые типа а и г (рис. 2.6) не представляют интереса, поскольку соответствуют случаям, когда сквозь зазор либо протекает полный ток, либо ток вообще не протекает. Случай, показанный на кривой б, легко получается при решении двух согласованных уравнений Чайлда. Случай, соответствующий кривой в, интересен и требует дальнейшего обсуждения, поскольку в определенных ситуациях он приводит к устойчивому потоку при двух значениях тока, т. е. к бифуркации устойчивого решения.

уравнений разд. 2.5 можно найти значение J, соответствующее значению потенциала V₀в минимуме. Пусть V₁и V₂— потенциалы, промежуточной сетки и коллектора, при этом η₁ = V₁/V₀и η₂=V₂/V₀. Пусть а — ширина, зазора между сеткой и коллектором, а₁ — расстояние между инжектирующей сеткой и точкой минимума потенциала. Из (2.47) получим

                                                                                 (2.51)

                                                                    (2.52)

где λ=V₂/ V ₁= η₂/ η_1. Из (2.51), (2.52) следует

                                                    (2.53)

Подставив выражение    для х₀ из   (2.41б)  при  V₀=V₁ /η₁ и разрешив его относительно плотности тока J, найдем

                                                                     (2.54)

где J₀=χ,V₁^3/2/a² — ток Чайлда — Ленгмюра,    соответствующий напряжению V₁и зазору а.

Рассмотрим для простоты случай V₂ = V₁, когда  λ=1. Тогда из (2.54) имеем

                                                                (2.55)

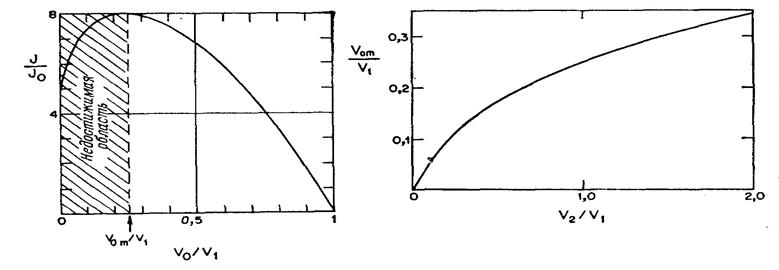На рис. 2.7 изображен график функции J /J₀в зависимости от аргумента 1 /η₁ = V₀/V₁; следует отметить, что ток проходит через максимум при величине V₀=V_0m. В нашем частном случае V_0m=V₁/4, но в общем случае V_0mзависит от  λ =V₂/V₁, как показано на рис. 2.8. Можно видеть, что распределение потенциала при 0<V₀<V_0m недостижимо. Представим, например, что значения V₁ и V₂фиксированы и увеличивается плотность тока. При этом V₀ уменьшается вплоть до значения V₀ = V_0m .Дальнейшее увеличение тока инжекции будет сопровождаться отражением и приведет к кривой типа б на рис. 2.6. Если теперь ток инжекции уменьшается, пропускаемый ток будет нарастать до тех пор, пока минимум не удалится на наибольшее расстояние от плоскости инжекции, когда пропускается наибольшая часть эмитируемого тока. При V₂ = V₁минимум расположен в медианной плоскости и J =4J₀- Дальнейшее уменьшение тока инжекции вызовет скачкообразное изменение потенциала к кривой    типа в на рис. 2.6. При V₂ = V₁это состояние, как следует из рис. 2.7, соответствует  V₀ = 0,75V₁.

Распределения потенциала, соответствующие V₀ < V_0m, не получаются и при изменении напряжения. В качестве иллюстрации рассмотрим численный пример. Предположим, что электронный ток J₀ = 0,l А/см² инжектируется сквозь тонкую сетку при потенциале V₁= 100 В относительно точки старта электронов. Плоский коллектор параллелен сетке и отстоит от нее на расстоянии а = 0,4 см. Найдем вольтамперную J — V-зависимость для коллектора вначале при нарастающем от нуля напряжении вплоть до насыщения, а затем, когда напряжение вновь спадает до нуля.

До тех пор пока часть тока отражается, имеем две кривые Чайлда: одну — для тока αJ₁и    другую — для тока (2— α)J₁. Ток  J₁ (2— α)  соответствует   напряжению     V₁ = 100 В,    а ток αJ₁— приложенному    напряжению    V₂ .   Используя    формулу(2.9а), имеем

                        J₁ (2— α) =  χ_eV₁^3/2/a²                                                                                                     (2.56)

                       αJ₁  =  χ_eV₂^3/2/(a— a₁)²                                                                                                   (2.57)