Бесстолкновительные явления при наличии пространственного заряда, страница 6

Рис. 2.5. Отношение толщины слоя при начальной энергии иона eV₀ к толщине слоя, полученной из уравнения Чайлда, а) при одинаковой энергии на коллекторе; б) при одном и том же падении напряжения в слое.

2.8. Плоская задача при наличии пространственного заряда в общей постановке

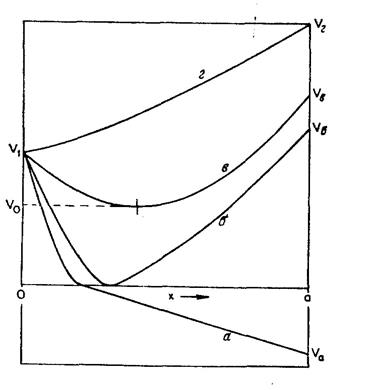
Задача о движении заряженных частиц, инжектированных с заданной энергией eV₁ в зазор между двумя параллельными электродами, которая подобна рассмотренной в разд. 2.5, но без нулевого поля на одной из границ, была решена в 1938 г. [238, 85J. В общем случае существуют четыре возможных типа решений (рис. 2.6). Как и в разд. 2.7, потенциал отсчитывается от точки, в которой электроны покоятся. Рассмотрим вначале случай, представленный кривой а. Здесь потенциал правого электрода отрицателен он электроны не могут на него попасть. Все электроны отражаются в точке нулевого потенциала, и эта точка может рассматриваться как виртуальный катод, ограниченный по эмиссионной способности и эмитирующий ток 2J, где J — ток, инжектированный при х = 0.

	Рис. 2.6. Типы распределений потенциала между параллельными плоскостями при инжекции слева направленного потока электронов с энергией eV1. Кривая а соответствует потенциалу коллектора <0, когда все электроны отражаются. В случае б потенциал коллектора таков, что часть α(0<α<1) инжектированных электронов достигает плоскости х = а. В случае в между плоскостями существует минимум потенциала V0 > 0. Кривая г соответствует монотонному ускорению в пространстве между плоскостями. При этом также возможно Vг<V1, когда происходит монотонное замедление и все электроны достигают коллектора

Решение в области между виртуальным катодом и плоскостью х = 0 — это решение уравнения (2.4) при условии V' ≠ 0 на виртуальном эмиттере. В области между виртуальным эмиттером и плоскостью х = а производная V' постоянна и решение таково, что V' непрерывна на виртуальном  эмиттере.

На кривой б (рис. 2.6) потенциал обращается в нуль в некоторой точке, а на обеих границах V≥0. Вообще говоря, этот случай соответствует отражению части потока, хотя в пределе отражение может быть полным или вообще отсутствовать. В случае полного отражения потенциала  V_б=0, причем а ≥ x₀, где х₀ — длина Чайлда по току 2J и напряжению V₁ (см. задачу 2.11). Точка поворота возникает при значении х, удовлетворяющем уравнению Чайлда при токе 2J и напряжения V₁ . Случай, отображаемый кривой б, может иметь место и при отсутствии отражения, если два решения уравнения Чайлда, соответствующие одному и тому же току J, полностью совпадают. В общем кривая типа б соответствует пропусканию тока αJ при 0<α<1; полное решение получается при сшивке в заданной области пространства при заданном напряжении решения Чайлда для тока (2—α)J слева от точки минимума и для тока αJ справа от нее. Эта ситуация описана, например, в задаче 2.3.

В случае кривой в (рис. 2.6) между двумя плоскостями возникает минимум, но минимальный потенциал V=V₀ > 0. Отражение частиц отсутствует, а решение дается в виде двух зависимостей типа (2.48) при одном и том же токе J и энергии инжекции eV₀ . В пределе, когда минимум расположен на одном из электродов, решение точно соответствует случаю, рассмотренному в разд. 2.7. Наконец, кривая г отображает ситуацию, когда электроны все время ускоряются, и соответствует решению уравнения (2.4) при положительных V и dV/dx в точке х = 0. Хотя потенциал коллектора, показанный на рисунке, выше, чем потенциал инжекции V₁ потенциалы V_б, V_в и V_г, кривых б, в, г могут быть и меньше V₁.