Бесстолкновительная плазма. Дебаевская длина экранирования

Глава 3

БЕССТОЛКНОВИТЕЛЬНАЯ ПЛАЗМА

3.1.  Краткое содержание

Почти во всех сильноточных ионных источниках ионы возникают в плазме[1]. Таким образом, важно изучить свойства этой среды как источника ионов, в том числе связь между плотностью ионного тока и параметрами плазмы и ожидаемое распределение ионов по энергиям в пучке, возникающем из плазмы. Распространение волн в плазме — одна из главных тем большинства книг по плазме — приводится здесь только в виде краткого обзора, а плазменные неустойчивости не рассматриваются совсем.

3.2.  Образование плазмы

Рассмотрим, следуя Ленгмюру [172], область между двумя плоскими параллельными электродами, один из которых расположен в точке х = 0 и имеет потенциал V=0, другой — в точке х = апод потенциалом V=V_а. Предположим, что ионы образуются с постоянной скоростью gв единице объема во всем межэлектродном пространстве. При этом всякий раз при рождении иона появляется и электрон, но давайте на некоторое время пренебрежем вкладом электронов в пространственный заряд. До тех пор, пока потенциал в пространстве изменяется монотонно, электроны уходят из межэлектродного зазора настолько быстро по сравнению с ионами, что пренебрежение их вкладом в пространственный заряд оправданно. Предположим также, что образуются покоящиеся ионы. Последнее предположение оправдано тем, что энергия нейтральных атомов относительно мала и тем, что при столкновении с электроном иону передается малая доля кинетической энергии.

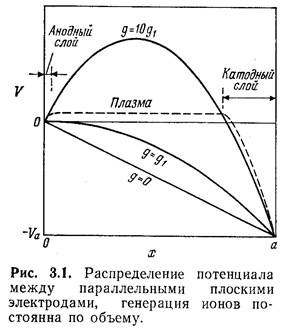
По мере увеличения скорости ионизации gраспределение потенциала будет изменяться от линейного при g = 0до распределения, при котором dV/dx=0при х= 0(рис. 3.1). Обозначим для последнего случая соответствующую скорость ионизации g_i. Дальнейшее увеличение gдолжно привести к возникновению максимума потенциала, см. кривую g=10 g₁(рис. 3.1). Но в этом случае предположение о пренебрежимо малом вкладе электронов в пространственный заряд и в распределение потенциала уже не справедливо.

В действительности электроны захватываются и должна образоваться плазма. Вернемся к этому позже. Найдем сначала критическое значение g_i, соответствующее переходу от состояния, когда ионы и электроны уходят из объема по мере их появления, к образованию плазмы.

Удобно применить для анализа метод баланса импульса (см. разд. 2.3). Поскольку на положительном электроде нет ни тока, ни поля, на него не действует никакая сила. Поставим условие, чтобы на электроде в точке под потенциалом V(x)поток кинематического импульса в единицу времени был точно равен электростатической силе притяжения e₀ V’²/2на единицу площади. Плотность тока, приходящего из интервала dx₁ около точки Х₁в точку х, равна

dJ = g₁edx₁.(3.1)

Она создается частицами со скоростью

(3.2)

где V₁— потенциал в точке x₁. Поскольку dJ/e  есть число ионов в секунду, получим, умножая эту величину на, поток импульса за секунду. Затем проинтегрируем его по x₁и будем иметь уравнение

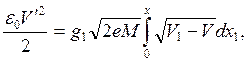
или

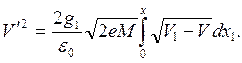                                              (3.3)

Простейшая кривая типа кривой для g = g₁на рис. 3.1 задается зависимостью

V = -V_ax²/a²(3.4)

Это выражение является решением уравнения  (3.3). Тогда получим

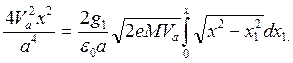                                     (3.5)

Заменив x₁=xSinq, найдем

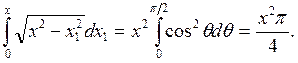
Подставив результат в (3.5), можно заметить, что  (3.4) — решение уравнения (3.3), и

                           (3.6)

Интересны некоторые свойства этого решения. Текущий к отрицательному электроду ток

J₁ = g₁ea(3.7)

приводится к виду

                                              (3.8)

Как нетрудно заметить,

J₁=(9/p)J₀=2.865J₀ ,                                                              (3.9)

где J₀ — ток Чайлда — соответствующий напряжению V_aи зазору а. Плотность объемного заряда, равная, согласно уравнению Пуассона, величине —e₀V", есть

ρ = 2e₀V_а/а²                                                                        (3.10)

и не зависит от х.

При g>g₁и сделанных предположениях должно получиться решение типа кривой g=10g₁на рис. 3.1. Его можно найти, сшивая два решения типа (3.4), чтобы получить параболическую зависимость с максимумом между х = 0 и х = а. Оно имеет вид

V= - V_a(x/a)[1-(g/g₁)^2/3(1 – x/a)],                                         (3.11)

но эта зависимость не наблюдается. Всякий раз при рождении иона появляется свободный медленный электрон. Такие электроны будут захватываться вблизи максимума потенциала, т. е. предположение о пренебрежимо малом вкладе электронов в пространственный заряд оказывается несправедливым. В действительности заполнение области с максимумом потенциала электронами приведет к образованию области, в которой плотности пространственного заряда ионов и электронов примерно равны, а потенциал приблизительно    постоянен     (штриховая кривая на рис. 3.1). Среда, в которой плотности    пространственного заряда ионов и электронов примерно равны, называемая плазмой, существует, если потенциал    в ней достаточно положителен относительно положительного электрода   (V=0), так что электроны покидают объем с той же скоростью, с какой  появляются.  Если  падение потенциала  в  области, называемой анодным слоем, стремится к нулю, то электроны уходят из объема столь быстро по сравнению с ионами, что должен возникнуть максимум в распределении потенциала. Необходимое равновесное состояние разряда обеспечивается образованием области с очень малым полем под положительным потенциалом относительного анода   (рис. 3.1). Плазма возникает, если g>g₁. Механизмы, обеспечивающие дрейф ионов к границам плазмы, будут частично рассмотрены в разд. 3.4и 3.5.