Бесстолкновительная плазма. Дебаевская длина экранирования, страница 12

При  величина  и правая часть в (3.83) должны совпадать, и можно не вычислять С₀ или сделать это для проверки. Третьим членом в скобках можно пренебречь по сравнению с первыми двумя, тогда получим

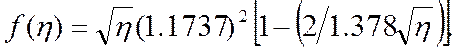                                        (3.87)

Из (3.79) следует

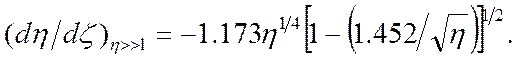                              (3.88)

Сравнение показывает, что необходимы очень большие значения ηдля того, чтобы градиент потенциала из уравнения Чайлда, задаваемый (3.83), приблизился по величине к наклону кривой решения в слое, которое определяется выражением (3.89) при больших η. Например, при η = 50 наклон кривой Чайлда больше истинного на 10 % и даже приη= 100он больше на 7%. Чтобы наклон не отличался более чем на 1 %, требуется η ~ 5000.

При η>20 уравнение (3.88) является хорошей аппроксимацией, так что получим

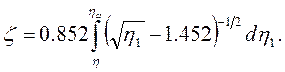
Это выражение можно проинтегрировать, тогда имеем

                 (3.89)

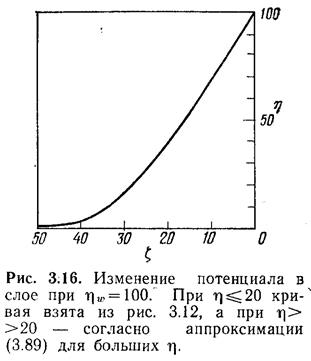
На рис. 3.16 показан ход потенциала при ; при  использовано соотношение (3.89), а при η >20 —значения на кривой рис. 3.12. Совпадение наклона кривых в точке η = 20 подтверждает пригодность (3.89) для значений η >20.

3.9. Прикатодный двойной слой

Если граничащая с плазмой поверхность под отрицательным потенциалом эмитирует электроны, то распределение потенциала и толщина слоя изменятся. Предельный случай катода с эмиссией, ограниченной пространственным зарядом, был детально изучен авторами работы [57]. Если падение потенциала в слое значительно больше, чем kT_с/e, где Т_с— температура катода, то можно считать, что электроны испускаются с нулевой скоростью. Тогда со стороны катода слой похож на показанный на рис. 2.14 и проанализированный в разд. 2.10. Однако со стороны плазмы имеются существенные отличия и сохраняются все сложности, отмеченные в разд. 3.8: распределение ионов по скоростям и пронизывание слоя электронами плазмы.

Ограничимся вычислением в данном случае отношения электронного тока к ионному, т. е. выяснением того, как изменится уравнение (2.96), если эмитирующую ионы границу заменить плазмой. Обратимся вновь к закону сохранения потока импульса (разд. 2.5).

Вместо того чтобы рассматривать задачу в точной постановке, упростим ее, предположив, что все ионы приходят на границу слоя с бомовской энергией kT/2, полученной из уравнения (3.27), и что соответствующая плотность ионного тока, согласно (3.28), есть, где n_р— плотность ионов или электронов в переходной области плазма — слой. Заменим поверхность плазмы твердой поверхностью, которая испускает направленные ионы и максвелловские электроны. Полное давление на эту поверхность складывается из трех слагаемых: отдачи от инжектированных ионов, давления максвелловских электронов и передачи импульса электронами из катода

Но из   (3.28)   следует, что это дает

(3.90)

Сила, действующая на катод, обусловлена только передачей импульса ионами

                                                       (3.91)

При kT/2eV<<1это выражение можно переписать в виде

                                              (3.92)

Поскольку силы F_pи F_cнаправлены    противоположно, получим

                                        (3.93)

Опустив малый в сравнении с единицей член kT/4eV, но сохраняя, имеем

(3.94)

Различие между (3.94) и (2.96) может быть существенным. Например, в типичном плазменном источнике ионов величина kT/eVможет быть равна 0,1, что уменьшит J_e/J_i до .

Хотя обычно предполагается, что используемые в ионных источниках разряды существуют в условиях эмиссии, ограниченной пространственным зарядом, когда применимо уравнение (3.94), создаваемое эмитированными электронами охлаждение (более подробно этот вопрос обсуждается в разд. 7.4) вызывает на этот счет большие сомнения. Если электронная эмиссия возрастает до величины, когда нагрев ионами точно компенсируется охлаждением электронами, то электронная эмиссия составит не более половины величины, даваемой уравнением (3.94).

3.10. Плотность нейтрального газа