Бесстолкновительная плазма. Дебаевская длина экранирования, страница 5

       ξ=x/L,                                                                       (3.34)

где L— некоторая длина, которую следует выбрать таким образом, чтобы упростить задачу. Заметив, что коэффициент в первом члене уравнения (3.33) есть квадрат дебаевской длины, λ_D , получим

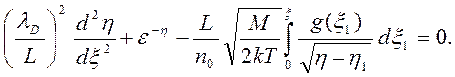                              (3.35)

Можно ожидать, что это уравнение справедливо от стенки до стенки, т. е. в плазме и слоях; назовем его полным уравнением плазма — слой.

Интегрируя уравнение (3.35), автор работы [247] пришел к дифференциальному уравнению первого порядка. Получим это уравнение методом баланса импульса (см. разд. 2.5). Использование одновременно уравнения Пуассона и метода баланса импульса является излишним, но, как увидим далее, полезно иметь обе формы уравнения плазма — слой. Для того чтобы применить метод баланса, рассмотрим диод на рис. 3.4.

Пусть левая плоскость будет плоскостью х=0на рис. 3.3 а правая — плоскостью под потенциалом V(x).Если эти плоскости неизменны, то у каждой из них плазма эмитирует электроны с той же скоростью, с которой они достигают поверхности, и при той же температуре. Возникающее электронное давление p = nkTравно n₀kTна левой плоскости и n₀kT exp(eV/kT)на правой. Единственной силой, действующей на левую плоскость, является электронное давление, но на правую, как следует из рис. 3.4, действует также ионное давление, обусловленное ионной бомбардировкой, и электрическое натяжение. Приравнивая сумму всех дав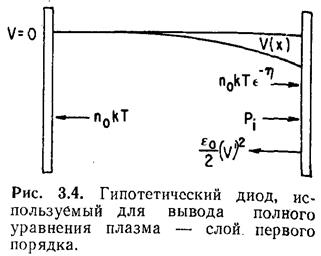лений нулю, получим

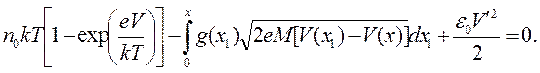
Заменив Vнаηсогласно  (3.31), а x  - на ξ (3.34) и разделив на n₀kT, имеем уравнение

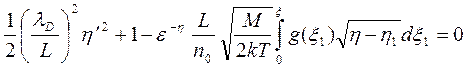,                                     (3.36)

т. е. искомое дифференциальное уравнение первого порядка. В решении задачи 3.4 показана эквивалентность уравнений (3.35) и (3.36).

Удобно представить gв виде

,                                                                       (3.37)

где v — константа, а γ — величина, характеризующая процесс ионизации. Случай γ= 0 соответствует постоянной скорости ионизации g = vn₀, т. е. ситуации, когда превалирует ионизация первичными электронами. В случае γ=1 ионизация пропорциональна плотности электронов, т. е. v — число возникающих за секунду ионов на один электрон. В случае γ= 2 имеем ионизацию из возбужденного состояния, и число возбужденных атомов пропорционально плотности электронов. Если положить

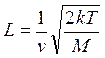,                                                                    (3.38)

то полное уравнение плазма — слой  (3.35)   можно записать в виде

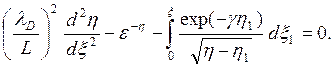(3.39)

Далее найдем связь Lс шириной камеры, но приблизительную оценку Lможно сделать еще до нахождения решения. Можно переписать (3.38) в виде

                                                  (3.40)

Согласно критерию Бома, на границе плазмы . Плотность ионов на границе примерно вдвое меньше n₀. Таким образом, правая часть (3.40) равна примерно утроенной плотности ионного тока. Произведение vn₀есть скорость рождения ионов в центре плазменного объема. Тогда оказывается, что Lпримерно равна утроенной полуширине аплазмы.

В лабораторных условиях 10^{-3 см} <λ_D< 10^{-1 см}, если L~10 см, то величина (λ_D/L)²лежит в диапазоне между 10^-8 и 10^-4. Если производная d²η/dξ² не слишком велика по сравнению с единицей, т. е. мала по сравнению с величиной e ^-η в центральной области плазмы, первым членом в (3.39) можно пренебречь и получить уравнение плазмы

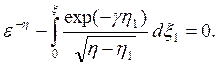                                                  (3.41)

Отбрасывание члена с d²η/dξ² в (3.39) эквивалентно предположению n_e = n_iи определяет плазменное приближение. Использование плазменного приближения упрощает анализ, но для оценки диапазона применимости плазменного решения следует оценить отброшенное слагаемое, а полное уравнение плазма — слой понадобится для сшивки плазмы со слоем.

Заменяя переменные соответствующим образом, Харрисон и Томпсон [124] привели уравнение (3.41) к виду, допускающему использование преобразования Шлёмильха. Таким образом, они получили решение ξ(η)в конечном виде. Оно приведено для трех случаев, представляющих особый интерес: