Бесстолкновительная плазма. Дебаевская длина экранирования, страница 15

Если в качестве простого упражнения читатель представит, что ионы плазмы закреплены в пространстве и их плотность однородна, а плотность электронов неоднородна вмалой степени, то можно показать, что электроны будут осциллировать около положения равновесия с характерной угловой частотой

                                                      (3.110)

Если пренебречь тепловым движением электронов, то эти возмущения не распространяются, но учет электронной температуры приводит к дисперсионному уравнению Бома — Гросса (здесь оно не приводится), которое описывает распространение электронных волн.

Дисперсионное уравнение распространения электромагнитных волн в плазме без магнитного поля имеет вид

                                                        (3.111)

где k— волновой вектор, входящий в выражение expj(kx—ωt), описывающее волну с частотой ω, которая распространяется в направлении +хс фазовой скоростью ω/kи групповой скоростью dω/dk.В (3.111) kпри любом ω<ω_p является мнимым, что означает полное отражение волны, падающей на поверхность плазмы.  В этом случае имеем соотношение

                     (3.112)

описывающее малые колебания с амплитудой, экспоненциально затухающей в пространстве на расстоянии

                                                             (3.113)

В типичном ионно-плазменном источнике n = 5∙10¹⁷ м^-3, что приводит к ω_p= 4∙10¹⁰ с^-1, или к частоте f_р=6,3 ГГц. Очевидно, что в плазму, представляющую интерес для ионных источников, проникают волны в микроволновом диапазоне. Если частота ω<ω_p, но не слишком близка к ω_p, то глубина проникновения δ составит ~ 1 см. Это расстояние настолько мало для плазмы интенсивных ионных источников, что излучение можно считать непроникающим.

Если плазма находится в магнитном поле, то в дополнение к частоте ω_p появляется набор характерных частот. Колебания электронов вдоль магнитных силовых линий не возмущаются и их частота по-прежнему равна ω_p. Комбинация электрических и магнитных сил, действующих на электроны, которые смещаются поперек магнитного поля, приводит к возникновению колебаний с частотой

                                                           (3.114)

которая называется верхней гибридной частотой. Величина

                                                                  (3.115)

есть электронная циклотронная частота в статическом магнитном поле напряженностью В₀.

Для того чтобы описать распространение электромагнитных волн в плазме при наличии магнитного поля, необходимо ввести еще две характерные частоты ω_L и ω_R,определяемые соотношением

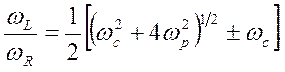                                       (3.116)

Поведение электромагнитных ноли в плазме можно списать   следующим   образом   в терминах частот ω_p,   ω_c,  ω_h,  ω_L,   ω_R.

Случай 1. Распространение  | В₀, Е||В₀. При этом отсутствует  магнитная    сила, обусловленная     электрическим полем волны. Пригодно выражение  (3.111). Частотыω < ω_p отражаются, плазма прозрачна   для   частот ω < ω_p   (если пренебречь столкновениями).

Случай 2. Распространение | Bo, E |  B₀. В диапазонах 0< ω < ω_L, ω_h < ω< ω_R волны не распространяются. Существует резонанс (поглощение энергии электронами) при ω=ω_h.

Случай 3. Распространение || В₀, левая (против часовой стрелки) поляризация. Волны не распространяются приω < ω_Lи не поглощаются при ω >ω_L.

Случай 4. Распространение || В_с, правая поляризация. Волны не распространяются при ω_c<ω<ω_R, поглощение отсутствует при ω<ω_R. Существует резонанс (поглощение энергии электронами) при ω =ω_с.

Задачи

Раздел 3.2

3.1. Разрядная трубка состоит из двух плоских электродов, помещенных в стеклянную трубку (рис. 3.19). Пусть разность потенциалов между электродами равна 5000 В, в трубке находится аргон, подсвечиваемый ионизующим (ультрафиолетовым) излучением.