Бесстолкновительная плазма. Дебаевская длина экранирования, страница 4

Прежде чем проводить анализ,   полезно сделать несколько замечаний относительно природы    плазмы.    Поскольку ионы должны достигать границы    плазмы,    т. е. границы объема, в котором , со средней энергией, большей kT/2, следует ожидать, что потенциал в плазме изменится на величину, равную примерно    kT/e, где Т — электронная    температура.    Поскольку плотность    электронов    в плазме    пропорциональна exp(eV/kT),можно ожидать ее изменения в 2—3 раза. Существование электронов с максвелловским распределением вплоть до самой границы плазмы накладывает требование, чтобы плазма находилась под достаточно высоким потенциалом относительно границы,  т. е. чтобы    отражались    практически    все электроны; в противном случае их максвелловское распределение окажется обрезанным. В разд. 3.8 показано, что хаотический поток электронов в плазме    настолько велик по сравнению с ионным потоком, что не будь плазма    под потенциалом в несколько kT/eотносительно стенок, электроны уходили бы из нее гораздо быстрее, чем ионы.

Когда быстрые первичные электроны из катода попадают в плазму, их энергия на порядок выше kT. Плотность этих электронов в плазме нечувствительна к относительно малым изменениям потенциала в объеме. Если ионизация вызвана первичными электронами, то, даже если    их плотность    составляет лишь малую часть общей плотности электронов, скорость ионизации будет постоянной в объеме при постоянной    плотности нейтральных атомов. Если, с другой стороны, основным типом взаимодействия первичных электронов является их взаимодействие с максвелловскими электронами    и ионизация в основном производится    высокоэнергичными    электронами    хвоста максвелловского распределения, то скорость ионизации в единице объема будет пропорциональна плотности электронов. Наконец, если ионизация максвелловскими электронами идет в основном из возбужденного состояния атомов, плотность которых пропорциональна n_е, то следует ожидать, что скорость ионизации будет пропорциональна n_е². Следуя Тонксу и Ленг-мюру [269], обсудим все три случая.

А. Плоская геометрия

Вначале рассмотрим детально плазму, созданную между двумя плоскими параллельными электродами под одним и тем же потенциалом, находящимся на расстоянии 2адруг от друга. Далее обсудим и другие конфигурации. Ожидаемое распределение потенциала показано на рис. 3.3; потенциал очень слабо спадает в области плазмы, где плотности ионов и электронов примерно равны, и на границе имеется слой с толщиной порядка дебаевской длины экранирования, в котором явно превалируют ионы. Предполагается, что поля, перпендикулярные плоскости рис. 3.3, равны¹ нулю.

Распределение потенциала V(х)должно удовлетворять уравнению Пуассона (3.13), причем плотность электронов задается уравнением Больцмана (3.12), а плотность ионов была введена в разд. 3.2. Обозначим скорость генерации ионов, т.е. число ионов, возникающих в единице объема в единицу времени, через g(x). Тогда плотность на расстоянии хот медианной плоскости получим, интегрируя по всем ионам, возникающим между этой плоскостью и плоскостью, проходящей через точку х, с учетом их скорости, соответствующей падению потенциала от точки рождения до точки х. Таким образом,

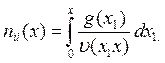(3.29)

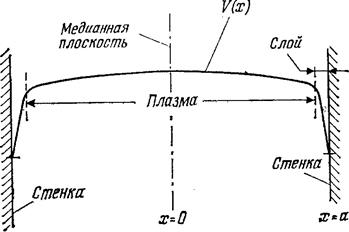
Рис. 3.3. Ожидаемое    распределение потенциала в плазме между плоскими параллельными стенками.

В бесстолкновительном случае, т. е. тогда, когда ионы, возникнув, движутся к стенкам без столкновений[3], как и в разд. 3.2, можно положить

                                                   (3.30)

Записывая vв виде (3.30), полагаем, что ионы рождаются с нулевой скоростью. Упростим рассмотрение, введя безразмерный потенциал

,                                                            (3.31)

где Т — электронная температура, тогда

,                                              (3.32)

Где  а . Уравнение Пуассона, где Vзаменено на η, после умножения на (ξ₀/n₀e) запишем в виде

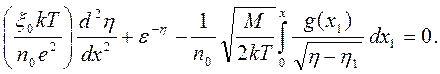                                (3.33)

Выберем η=0 при х=0, так что n₀есть плотность электронов в медианной плоскости. Перейдем к безразмерной координате