Бесстолкновительная плазма. Дебаевская длина экранирования, страница 2

3.3. Дебаевская длина экранирования

Измеряя вольт-амперные характеристики I(V)малых зондов, помещенных в плазму, Ленгмюр [171] смог установить, что распределение электронов по энергии в плазме — максвелловское в широком диапазоне параметров, даже когда быстрая термализация не может быть объяснена столкновениями между частицами[2]. Соответственно 'плотность п_е электронов в плазме связана с потенциалом Vуравнением Больцмана

n_e = n₀exp(eV/kT),(3.12)

где n₀— плотность в толще плазмы, где полагаем V=0. Температура Т выражена в градусах Кельвина, k— постоянная Больцмана.

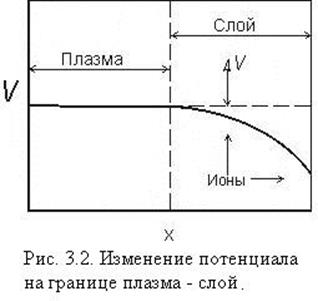
Рассмотрим для простоты одномерное изменение потенциала, которое существует, например, вблизи поверхности плоского электрода, погруженного в плазму. Запишем уравнение Пуассона

d²V/dx²= - e(n_i-n_e)/e₀,                                              (3.13)

предполагая ионы однократно заряженными. Положим потенциал Vравным нулю глубоко в плазме, где n_i=n_e=n₀. Предположим, что n_i- не зависит от потенциала, а n_e. определяется выражением (3.12). Тогда получим

d²V/dx²= - en₀[1 – exp(eV/kT)]/e₀.                                     (3.14)

При  eV/kT<<1можно  положить     exp(eV/kT) = 1+ (eV/kT)и получим линеаризованное уравнение

d²V/dx² = (n₀e²/e₀kT) V,             (3.15)

решениями которого являются зависимости

V = exp[±(x/λ_D)].                                                      (3.16)

Здесь

                 (3.17)

и называется дебаевской длиной экранирования.

Обычно размеры,    плазмы  >>  и положительный знак в (3.16) можно опустить.

Чтобы найти распределение потенциала в окрестности точечного заряда qв плазме, следует записать уравнение (3.14) в сферических координатах, линеаризуя которое при eV/kT<<1, получим

                                                       (3.18)

вместо обычной зависимости (q/для потенциала в вакууме.

Как можно видеть, — это расстояние, в пределах которого электростатический потенциал может оказывать сильное влияние на заряженные частицы. В плазме, получаемой в лабораторные условиях, это расстояние обычно составляет 0,01— 1 мм, но в принципе оно может быть произвольным. Наиболее важный критерий того, чтобы ансамбль заряженных частиц можно было назвать плазмой, таков: дебаевская длина должна быть мала по сравнению с размерами плазмы. В разд. 3.2 неявно предполагалось, что электроны — достаточно холодные, так что анодный слой, толщина которого порядка дебаевской длины, является достаточно тонким. Если >а, то могут существовать распределения потенциала подобно кривой g=10g₁на рис. 3.1. Удобно записать (3.17)  в виде

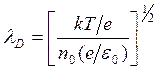,                                                           (3.19)

поскольку kT/e— электронная температура в электрон-вольтах (эВ) — единицах, обычно используемых в физике плазмы, а е/e₀= 1,8∙10^-8 В∙м—часто встречающаяся комбинация двух констант. Заметим, что здесь n₀— количество электронов в кубическом метре, а измеряется в метрах. В системе единиц, обычно используемой в лабораторных условиях, имеем

(см) = 745[T(эВ)/n₀(см^-3)]^1/2.                                              (3.20)

В сильноточных ионных источниках эВ, n₀— порядка 10¹² см^-3, что дает

2∙10^{-3 см.}

3.4. Критерий Бома

Для описания плазмы, которое проведено в двух предыдущих разделах, характерно примерное равенство плотностей электронов n_eи ионов n_iЭлектроны имеют максвелловcкое распределение, т. е. их можно характеризовать температурой.

Вначале     можно     предположить, что распределение ионов по скоростям    также    близко к максвелловскому,    так   что у них  тоже есть  своя температура,      а      взаимодействие электронов с ионами приведет к тому, что их температуры — величины     одного     порядка. Даже если ионная температура существенно       выше, поток электронов   сквозь   любое   сечение в плазме настолько больше ионного, что условие примерно одинакового ухода ионов и электронов из плазменного объема приводит к тому, что потенциал плазмы должен быть положительным относительно стенок. В этом случае все ионы, достигающие границы, ускоряются из плазмы вовне. Следовательно, все ионы плазмы, находящиеся от границы на расстояниях вплоть до некоторой длины пробега между столкновениями, движутся наружу, т. е. в направлении ближайшей границы. А это не согласуется с предположением о максвелловском распределении.