1) γ = 0, постоянная скорость ионизации:
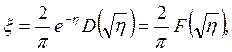 ξ0 =
0,3444; (3.42)
ξ0 =
0,3444; (3.42)
2) γ=1, ионизация, пропорциональная nе:
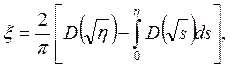 ξ0=0,3444; (3.43)
ξ0=0,3444; (3.43)
3) γ = 2, ионизация, пропорциональная nе2:
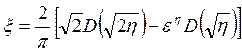 , ξ0=0,4920, (3.44)
, ξ0=0,4920, (3.44)
где интеграл
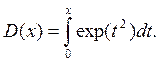 (3.45)
(3.45)
связан с функцией Доусона F(x), определенной согласно (2.129)[4].
Все
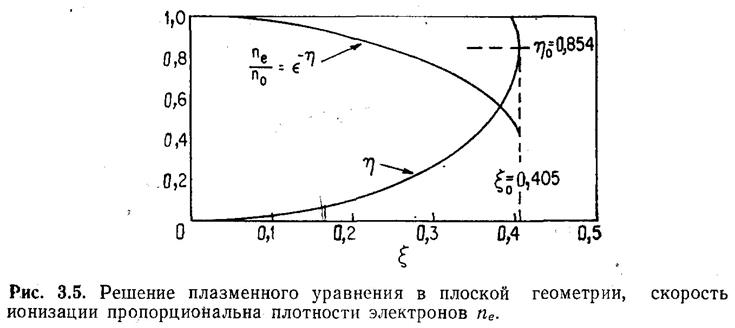
эти зависимости имеют вид, изображенный на рис. 3.5 для случая γ = 1. В каждом случае нижняя
ветвь двузначной кривой η(ξ) возрастает по мере роста ξ
до тех пор, пока не достигнет максимального значения ξ0 при η = η = 0,854, и затем
переходит в верхнюю ветвь по мере уменьшения ξ. Часть кривой η(ξ), соответствующая ![]() , не представляет интереса с физической
точки зрения. При
, не представляет интереса с физической
точки зрения. При ![]() в бесконечность стремится не
только
в бесконечность стремится не
только ![]() , но иd2η/dξ2,что делает некорректным
отбрасывание первого слагаемого в выражении (3.39). Точное решение должно иметь
вид, показанный на рис. 3.6, который отличается от плазменного решения в
области, где производная d2η/dξ2становится настолько
большой, что пренебрежение первым членом в уравнении (3.39) становится неоправданным.
, но иd2η/dξ2,что делает некорректным
отбрасывание первого слагаемого в выражении (3.39). Точное решение должно иметь
вид, показанный на рис. 3.6, который отличается от плазменного решения в
области, где производная d2η/dξ2становится настолько
большой, что пренебрежение первым членом в уравнении (3.39) становится неоправданным.
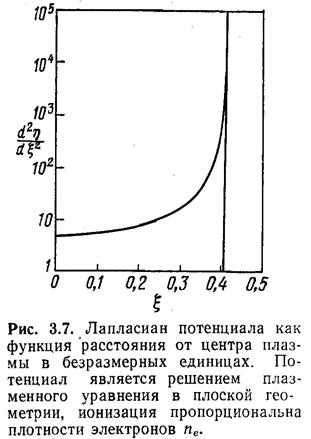
Место, где возникает отличие точного решения от плазменного, можно найти из рис. 3.7, на котором в виде функции нанесен график величины d2η/dξ2 зависимости (3.43) и использовано соотношение
![]() (3.46)
(3.46)
В
лабораторных условиях, когда 10-8<
(λD/L)2<10 -4условия применимости
плазменного приближения (ne = ni), т. е. отбрасывание
первого члена в уравнении (3.39), справедливы вплоть до очень малых
расстояний от границы. Точку, в которой следует ожидать отклонения от
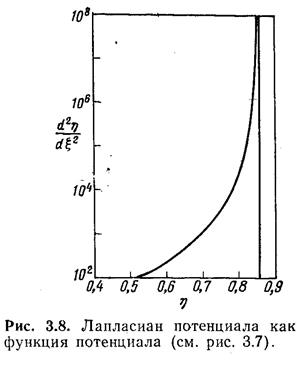
плазменного решения, легче определить из графика d2η/dξ2как функцию η(рис. 3.8). Например,
если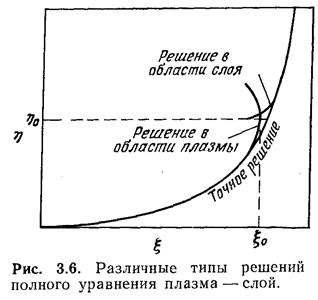 (λD/L)2=10
-5, то nеи niбудут различаться на 10 %
практически при ξ = ξ0 (см. рис. 3.6), но из рис. 3.7 следует, что при этом η = 0,78, а это существенно меньше η0 .Переход от .плазменного решения к решению в слое, который происходит
около этой точки, обсудим в разд. 3.8. Крутой наклон кривой, соответствующей
плазменному решению в точке его перехода к решению в слое, показывает, что
толщина слоя должна быть очень малой по сравнению с шириной плазмы а. В таком случае мы можем положить, что переменная ξ=x/Lна плазменной границе
будет иметь значение
(λD/L)2=10
-5, то nеи niбудут различаться на 10 %
практически при ξ = ξ0 (см. рис. 3.6), но из рис. 3.7 следует, что при этом η = 0,78, а это существенно меньше η0 .Переход от .плазменного решения к решению в слое, который происходит
около этой точки, обсудим в разд. 3.8. Крутой наклон кривой, соответствующей
плазменному решению в точке его перехода к решению в слое, показывает, что
толщина слоя должна быть очень малой по сравнению с шириной плазмы а. В таком случае мы можем положить, что переменная ξ=x/Lна плазменной границе
будет иметь значение
ξ0 = a/L, (3.47)
что дает при постоянной скорости ионизации
L = а/0,3444, (3.48)
при скорости ионизации, пропорциональной ne,
L = а/0,4046 (3.49)
И приg~ne2
L = a/0,4920. (3.50)
 Корректное
сравнение этих трех решений получается при нормировке на ξ0,
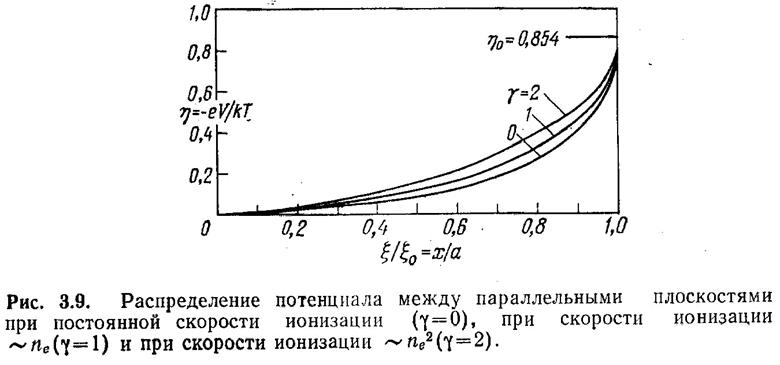
т. е. при нанесении графиков η в зависимости от ξ/ξ=x/a. Они представлены на рис. 3.9.
Корректное
сравнение этих трех решений получается при нормировке на ξ0,
т. е. при нанесении графиков η в зависимости от ξ/ξ=x/a. Они представлены на рис. 3.9.
Эти кривые очень похожи, было бы очень трудно выбрать нужную на основе экспериментальных данных и, насколько известно автору, никто не сумел определить потенциал плазмы в разряде в зависимости от расстояния с точностью, достаточной для выбора типа ионизации. Хотя некоторые исследователи (см., например, [269]) показали, что общее поведение потенциала согласуется с изображенным на рис. 3.9.
Б. Цилиндрическая и сферическая геометрии
Если плазма образуется в объеме, ограниченном цилиндрическими или сферическими границами, то вычисления проводятся по той же схеме, что и для плоской геометрии, но вместо уравнения (3.29) имеем
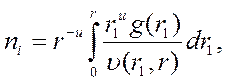 (3.51)
(3.51)
причем и=1для цилиндрической геометрии и и = 2 для сферической (случай и = 0 приводит к плоской геометрии и рассматривался отдельно). Как и в плоском случае, выберем в качестве п0 электронную или ионную плотность в центре, где потенциал, определяемый величиной η= -eV/kT, полагается равным нулю. Проведя выкладки, аналогичные приведшим к уравнению (3.35), имеем
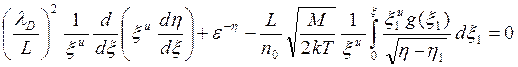 , (3.52)
, (3.52)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.