Б. Точное численное решение
Теперь
у нас имеются два решения полного уравнения плазма— слой, одно из них пригодно
в области плазмы, а другое описывает слой. Эти решения должны сшиваться подобно
тому, как показано на рис. 3.6. Селф [247] численно проинтегрировал уравнение
(3,35) и — с целью проверки —уравнение (3.36), которое он получил, интегрируя
(3.35). Его результаты для рассмотренных нами выше трех значений γи разных значений параметра ![]() приведены
в табл. 3.2. и изображены для случая γ =1
на рис. 3.13.
приведены
в табл. 3.2. и изображены для случая γ =1
на рис. 3.13.
Для того чтобы проверить полученные Селфом решения для слоя, приведем переменную ξ = x/Lк виду
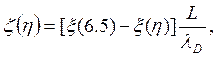
т.
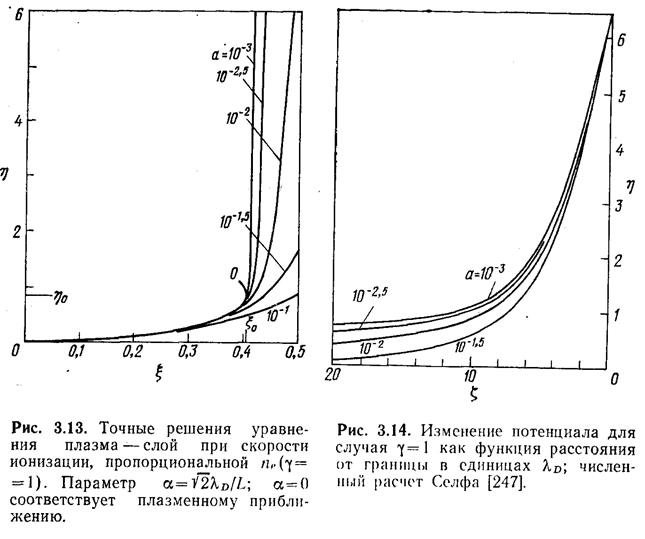
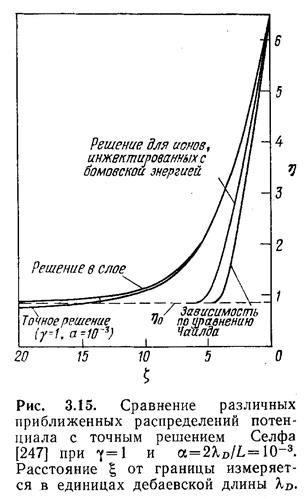
е. к расстоянию, измеряемому в направлении плазмы в единицах дебаевской длины λD; здесь ![]() выбрано нулевым при η= = 6,5. Полученные зависимости показаны на рис. 3.14, на рис. 3.15
кривая при α=10~3 сравнивается с решением в
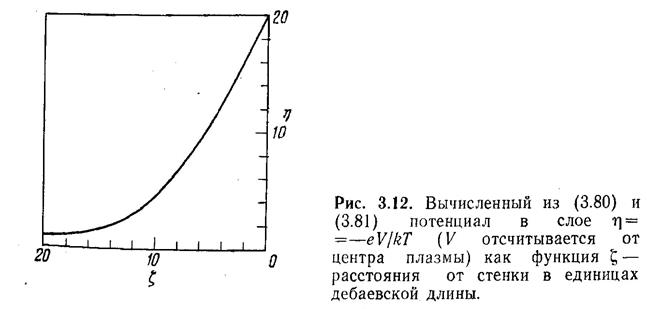
слое (рис. 3.12). Важно провести такое сравнение, поскольку кривая на рис.
3.12 обладает общностью, в то время как решения Селфа пригодны лишь для
конкретных значений γ и а.
выбрано нулевым при η= = 6,5. Полученные зависимости показаны на рис. 3.14, на рис. 3.15
кривая при α=10~3 сравнивается с решением в
слое (рис. 3.12). Важно провести такое сравнение, поскольку кривая на рис.
3.12 обладает общностью, в то время как решения Селфа пригодны лишь для
конкретных значений γ и а.
Как можно видеть, при α<10~3 потенциал в слое почти совпадает с асимптотическим решением, поэтому интересно знать параметры плазмы, соответствующие таким значениям α.
 Предположим,
что полуширина плазмы а = 0,1 м, т. е. L ~ 0,25 м. Тогда при α=10 -3 получим λD~ 1,77• 10 -4 м. Для типичной
лабораторной плазмы с kT/e=5BВ это соответствует
плотности 8,9∙1015 м -3 = 8,9∙109 см -3.
Это плазма весьма низкой плотности, ее плотность в 100 раз меньше плотности
плазмы, используемой в интенсивных источниках ионов. Кривая на рис. 3.12
позволяет рассчитать изменение потенциала в слое в широком диапазоне параметров
плазмы, получаемой в лабораторных условиях и практически для всех
ионно-плазменных источников.
Предположим,
что полуширина плазмы а = 0,1 м, т. е. L ~ 0,25 м. Тогда при α=10 -3 получим λD~ 1,77• 10 -4 м. Для типичной
лабораторной плазмы с kT/e=5BВ это соответствует
плотности 8,9∙1015 м -3 = 8,9∙109 см -3.
Это плазма весьма низкой плотности, ее плотность в 100 раз меньше плотности
плазмы, используемой в интенсивных источниках ионов. Кривая на рис. 3.12
позволяет рассчитать изменение потенциала в слое в широком диапазоне параметров
плазмы, получаемой в лабораторных условиях и практически для всех
ионно-плазменных источников.
Уравнение Чайлда вследствие своей простоты часто используют для оценки толщины слоя. Интересно проверить справедливость этого приближения. Пусть V0 — значение потенциала на границе плазма —слой, тогда из (2.8) и (3.69) получим
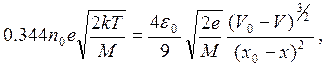
где х0—толщина слоя, а расстояние хотсчитывается от стенки.
Переходя
к η = —eV/kTи ![]() ,
запишем
,
запишем
![]() . (3.82)
. (3.82)
Взяв
η0 = 0,854, получим, положив
η = 6,5 при![]() , значение
, значение![]() . Как следует из рис. 3.15, такое решение
является грубой аппроксимацией; при η = 6,5 оно приводит к
толщине слоя, почти втрое меньшей значения, полученного при использовании
решения Селфа или при приближенном описании слоя.
. Как следует из рис. 3.15, такое решение
является грубой аппроксимацией; при η = 6,5 оно приводит к
толщине слоя, почти втрое меньшей значения, полученного при использовании
решения Селфа или при приближенном описании слоя.
При другом подходе, который легко осуществить и который усовершенствует рассмотрение на основе уравнения Чайлда, следует приписать ионам на границе слоя энергию Бома кТ/2и использовать (2.47). Согласно рис. 3.15, это приводит в рассматриваемом слое к толщине слоя, вдвое меньшей истинной толщины. Представленное на рис. 3.12 решение в слое также легко допускает грубые аппроксимации.
Трудно
получить точное значение толщины слоя. Для ее определения Селф предлагает
использовать точку η = η или ξ=ξ0. Однако в указанной области наклон кривой ![]() слишком
мал, чтобы придавать глубокий смысл полученному таким образом значению.
Например, из рис. 3.14 следует, что в масштабах дебаевской длины кривые при α= 10 -3 и α=10 -2,5 почти совпадают. Однако,
если использовать критерий η = η0то толщины слоя заметно
различаются. При
слишком
мал, чтобы придавать глубокий смысл полученному таким образом значению.
Например, из рис. 3.14 следует, что в масштабах дебаевской длины кривые при α= 10 -3 и α=10 -2,5 почти совпадают. Однако,
если использовать критерий η = η0то толщины слоя заметно
различаются. При ![]() Селф получает толщину слоя 14,8 λDдля случая α=10 -2,5 и 17,6λDдля случая α=10 -3.
Селф получает толщину слоя 14,8 λDдля случая α=10 -2,5 и 17,6λDдля случая α=10 -3.
Поскольку уравнение Чайлда столь часто используется для оценки толщины слоя, полезно посмотреть, насколько большой должна быть величина η, прежде чем это уравнение становится приемлемой заменой решения в слое. Используя уравнение Чайлда, из (3.82) получим соотношение
![]() (3.83)
(3.83)
Для
решения в слое этот градиент потенциала задается уравнением (3.79), так что
следует оценить f(η) при больших η. В (3.81) член ![]() , член
, член ![]() под
интегралом превращается в
под
интегралом превращается в ![]() ,
,![]()
![]() Тогда имеем
Тогда имеем
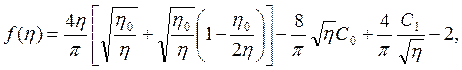 (3.84)
(3.84)
где
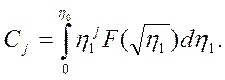 (3.85)
(3.85)
Вынося
![]() за скобки, получим
за скобки, получим
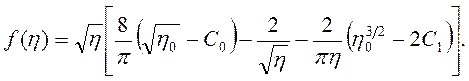 (3.86)
(3.86)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.