J = egLξ0, (3.68)
а из выражений (3.37) при γ = 0и (3.38) получим
![]() (3.69)
(3.69)
если использовать значение ξ0 = 0,344 согласно (3.42) для случая постоянной скорости ионизации. Подчеркнем, что (3.69) с той же константой 0,344 не зависит от величины γ,которая определяется типом ионизации.
Интересно
сравнить полученное выражение с током Бома (3.28). Поскольку ![]() близко к 0,5, можно думать, что Jiотличается примерно вдвое.
Однако плотность nрплазмы на границе примерно вдвое меньше n0и, таким образом, обе формулы
хорошо согласуются друг с другом.
близко к 0,5, можно думать, что Jiотличается примерно вдвое.
Однако плотность nрплазмы на границе примерно вдвое меньше n0и, таким образом, обе формулы
хорошо согласуются друг с другом.
Для цилиндрической геометрии Тонкс и Ленгмюр [269] нашли, что коэффициент в (3.69) равен 0,319, если g=const и 0,270, если g~ne.
Граница плазмы может быть обращена к поверхности электрода, к изолятору либо к апертуре (отверстию, щели), сквозь которую извлекаются ионы. По мере приближения к этой границе возникает область перехода от плазмы, где плотности ионов и электронов примерно равны, к слою, где, как следует из рис. 3.6, превалируют ионы. Из полного уравнения плазма — слой (3.35) невозможно найти какое-либо простое аналитическое решение в области перехода. Для каждого конкретного потенциала границы относительно плазмы можно легко оценить толщину слоя и изменение в нем потенциала, используя уравнение Чайлда (2.8) или уравнение (2.47) при значении V0 = kT/2e, которое получается из критерия Бома. Такой подход не учитывает проникновения электронов в слой и разброса ионов в слое по энергиям. Поэтому найдем более точные решения, которые можно будет использовать в качестве основы для выяснения степени точности простейших решений.
Прежде чем приступить к вычислениям, выясним, какой вид зависимости хода потенциала в слое следует ожидать. Большая величина электронного потока в плазме по сравнению с потоком ионов обычно приводит к тому, что плазма заряжается положительно относительно наиболее положительного электрода, который она легко может достичь. Обычно это — анод в разряде. Если граничащий с плазмой электрод находится под потенциалом катода, то в слое падает полное напряжение в разряде, обычно 50—100 В, плюс величина потенциала положительности плазмы относительно анода. Если электрод находится под плавающим потенциалом либо плазма граничит с изолятором, величина падения потенциала в слое должна быть такой, чтобы полностью сбалансировать ионный и электронный токи, т. е.
![]() (3.70)
(3.70)
где n0— плотность электронов в центре плазмы, a V0— потенциал этого центра относительно стенки. В уравнении (3.70) изначально предполагается, что практически все электроны максвеллизованы. Если в плазме присутствует заметное количество первичных электронов, то плавающий потенциал электрода приближается к катодному. С небольшой численной погрешностью из (3.70) получим
![]() (3.71)
(3.71)
 Отношение
массы иона к массе электрона можно заменить на 1836 МА,, где МА— масса иона в единицах
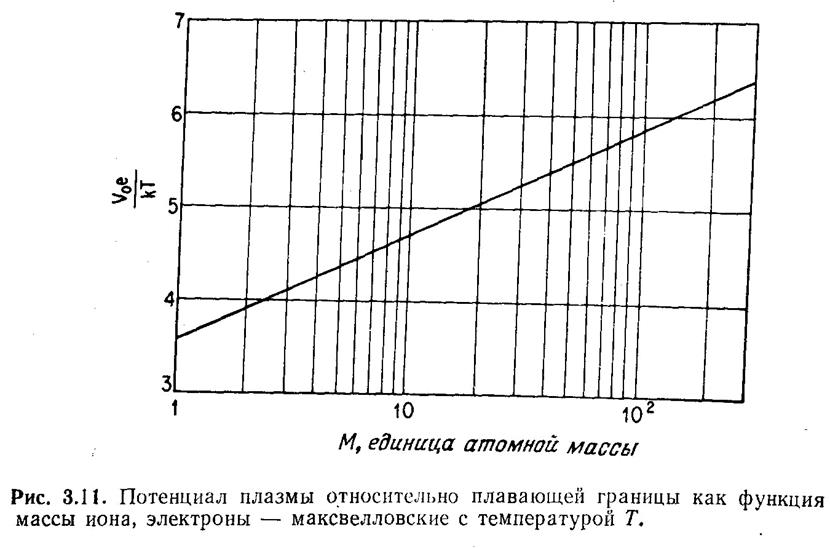
атомной массы. Это значение V0 как функция массы иона показано на графике (рис. 3.11). Как
можно заметить, в грубом приближении плазма находится под потенциалом 5kT/eотносительно стенки под
плавающим потенциалом. Поскольку электронный ток быстро возрастает с
уменьшением этого потенциала, падение потенциала между плазмой и анодом редко
бывает малым по сравнению с указанным значением.
Отношение
массы иона к массе электрона можно заменить на 1836 МА,, где МА— масса иона в единицах
атомной массы. Это значение V0 как функция массы иона показано на графике (рис. 3.11). Как
можно заметить, в грубом приближении плазма находится под потенциалом 5kT/eотносительно стенки под
плавающим потенциалом. Поскольку электронный ток быстро возрастает с
уменьшением этого потенциала, падение потенциала между плазмой и анодом редко
бывает малым по сравнению с указанным значением.
Предположим, что электроны в основном максвелловские и их плотность содержит больцмановский множитель ξ –η. Даже если равновесие устанавливается быстро, следует ожидать, что распределение уходящих от стенки электронов по скоростям должно быть обрезанным. Если потенциал стенки достаточно отрицательный, эффект будет незначительным, и потенциал на границе должен быть ниже потенциала на краю плазмы не менее чем на величину ЗkT/е (см. рис. 3.11).
Для
оценки предположим, что энергия ионов на границе пучка равна бомовской энергии kT/2, В точке, где потенциал
ниже указанного на величину![]() , плотность
ионов, согласно (3.23), равна
, плотность
ионов, согласно (3.23), равна
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.