Заряженные частицы в ЭМ поле. Заряд в потенциальном электрическом поле

Заряженные частицы в ЭМ поле

В вакуумном промежутке, где имеется электрическое поле с напряженностью Е и магнитное поле с индукцией В на частицу, имеющую заряд q действует так называемая сила Лоренца, которая в соответствие с законом Ньютона и определяет изменение импульса частицы

dp/dt = F_л  = qE + q[v x B]                                                    (1)

где v - скорость частицы.

Релятивистские эффекты могут быть важны в пучках частиц высокой энергии, в этом случае р=gmv, где g = 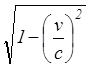- так называемый гамма – фактор, но в разрядах эти эффекты как правило не играют существенной роли, в этом случае р=mv без релятивистских поправок и (1) можно записать в виде

mdv/dt = qE + q[v x B]                                                                                    (1¢)

Вспомним некоторые частные решения этого уравнения.

Заряд в потенциальном электрическом поле

Пусть В = 0, а Е = - gradj, т.е. электрическое поле имеет потенциальный, не вихревой характер. Умножая обе части (1) на vdt и учитывая, что vdt=dr получаем

mvdv = qEdr = -qdj                                                           (2)

Интегрируя получаем хорошо известный закон сохранения энергии

mv²/2 - mv₀²/2 = -q(j - j₀ )                                                 (3)

Увеличение кинетической энергии равно уменьшению потенциальной. Здесь v₀  - скорость частицы в некоторый начальный момент времени, когда она находилась в точке, где потенциал равен j₀. Если начальная скорость мала (v₀ ~ 0), то кинетическая энергия равна произведению заряда на пройденную разность потенциалов, т.е на напряжение

e = q(j₀ - j) = qU,                                                               (4)

а скорость тогда определяется соотношением

v = (2qU/m)^1/2 .                                                                    (5)

Для электрона

v = 6×10⁵ ×U^1/2[м/с],

U в вольтах. Для иона

v = 1.4×10⁴(ZU/A)^1/2

где Z - кратность заряда иона, А - атомный номер.

Если электрическое поле однородное Е  ~  соnst, а магнитное по -прежнему отсутствует, то из уравнения (1) после интегрирования получается простая зависимость скорости от времени

v = v₀  + Et/m                                                                      (6)

v ~  Et/m при v₀ ~ 0.            

Заряд в однородном магнитном поле

Пусть Е=0, В=соnst, v_êç -продольная составляющая скорости в некоторый начальный момент времени, v- перпендикулярная к В составляющая. Тогда

mdv/dt =  q[v В],                                                              (7)

т.е. в плоскости перпендикулярной В за время dt происходит поворот вектора скорости на угол

da = çdvç/v = (qB/m)dt = wdt                                           (8)

где w = - так называемая Ларморовская частота. По абсолютной величине v не меняется. Также остается постоянной и продольная составляющая скорости. Таким образом вдоль магнитного поля происходит равномерное движение со скоростью v_çç, а в перпедикулярном направлении вращение с угловой скоростью w. При этом перпендикулярная составляющая радиус - вектора за время dt получит приращение

dr = vdt = vda/w                                            (9)

Вводя обозначение

R_л= v/w =  mv/qB                                              (10)

получим

da = çdrç/R_л                                                                            (11)

Конец радиус-вектора движется по окружности с радиусом R_л, так называемым Ларморовским радиусом. В случае электронов

w = 1.76×10¹¹В(Т)

R_л (см) = 3.4/В(Т)

а для ионов

w = 0.96×10⁸ZВ/А

R_л (см)= 1,46/ZВ(Т)

где А – атомный номер иона, Z – кратность заряда иона

Заряд в скрещенных полях ЕВ.

Пусть Е направлено вдоль оси х, а В вдоль z. Тогда имеем систему уравнений

mdv_х/dt = qE + qv_уB                                                           

mdv_у/dt = -qv_хB                                                                   (12)

mdv_z/dt = 0

Проще всего решается последнее уравнение v_z =v_z(0). Чтобы решить первое уравнение системы (12) поделим его на m и продифференцируем по времени

d²v_х/dt² = wdv_у/dt = - w²v_х.                                                    (13)

Тогда для v_х получается хорошо известное уравнение гармонических колебаний

,                                                                     (14)

решением которого являются комбинация гармонических функций

v_х = Сsinwt + Dcoswt                                                                      (15)

Постоянные зависят от начальных условий. Пусть v_х(0)=0, тогда D=0. Чтобы найти C положим v_y(0)=0. Тогда из первого уравнения системы (12) получаем

mdv_x(0)/dt = mwСcos(0) =qE                                                          (16)

Отсюда получаем

C = qE/mw = Е/В                                                                             (17)

Подставляя (15) во второе уравнение системы (12) поделим на m и интегрируя получим