Заряженные частицы в ЭМ поле. Заряд в потенциальном электрическом поле, страница 2

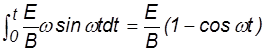v_у =                                           (18)

Итак, получаем, что вдоль оси z характер движения не меняется и определяется начальными условиями. Bдоль оси х, параллельно которой действует электрическое поле частица совершает колебательное движение. Вдоль оси у движение представляет собой сумму колебательного движения и направленного движения происходящего со скоростью Е/В. Поскольку в среднем скорость колебательного движения равна 0, то в целом происходит постепенный снос частицы в направлении оси у с постоянной скоростью или еще говорят происходит дрейф частицы. В данном случае это дрейф в скрещенных полях, происходящий со скоростью Е/В или в векторном виде

v_dr = [EB] / B²

Интересно отметить, что скорость дрейфа в скрещенных полях не зависит ни от заряда ни от массы частицы, а только от величин Е и В. В дальнейшем мы познакомимся и с другими видами дрейфа.

Элементарный ток при движении в промежутке одной частицы

Обсудим вопрос: что покажет гипотетический сверхчувствительный амперметр, включенный во внешнюю цепь, при пролете через промежуток одной заряженной частицы. Как известно при движении одной точечной частицы ток равен qd(r - r(t)) и казалось бы можно ожидать, что прибор будет показывать 0 до тех пор пока частица не перейдет из промежутка в электрод и не начнет двигаться во внешней электрической цепи. Однако при более внимательном рассмотрении можно сообразить, что при движении через промежуток электрон воздействуя своим электрическим полем на заряженные частицы, находящиеся на аноде, будет выталкивать их во внешнюю цепь. В то же время, по мере удаления электрона от катода и соответственном уменьшении создаваемого им на катоде электрического поля сюда будут подтягиваться частицы из внешней цепи и постепенно компенсируют в катоде недостаток заряда, возникший в результате вылета электрона из катода. Таким образом, во внешней цепи электроны будут двигаться от анода к катоду и этот ток и будет зарегистрирован амперметром. Рассчитать силу тока можно было бы, рассчитав изменение во времени электрических полей, но проще эта задача решается на основе энергетических соображений. Энергия, поставляемая источником питания за время dt

de = iUdt,                                                                                          (23)

затрачивается на совершение работы над движущейся заряженной частицей

dA = Fdх = eEvdt.                                                                            (24)

Приравнивая de к dA и учитывая, что

Е=U/d,                                                                                              (25)

где d - длина промежутка, получим

i = ev/d  ~  (e/d)Et/m                                                            (26)

Последнее выражение справедливо в том случае если электрон выходит из катода с нулевой скоростью и движется без столкновений, т.е. в вакуумном промежутке. Выражение i = ev/d имеет более общий характер и справедливо также и для газового промежутка. Полный заряд протекший во внешней цепи за время движения электрона от катода к аноду найдем интегрируя полученное выражение

q = i(t)dt                                                                                    (27)

Переходя от интегрирования по времени к интегрированию по координате dt=dx/v, получим

q = 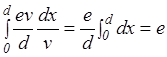.                                                                  (28)

Таким образом, при движении электрона через промежуток по внешней цепи также протечет один электронный заряд.

Если через промежуток летит одновременно несколько частиц, то ток во внешней цепи будет равен сумме по всем частицам

I(t) = Sev(t)/d.                                                                              (29)

При небольшом числе частиц, ток может довольно сильно флуктуировать вокруг некоторого среднего значения. Это так называемый дробовый шум, наблюдаемый в некоторых чувствительных устройствах.

Коротко обсудим вклад в ток, вносимый парой заряженных частиц, образовавшихся в некоторой точке х₀ внутри промежутка в результате ионизации. Заряд, протекший во внешней цепи, при движении такой пары заряженных частиц будет очевидно равен

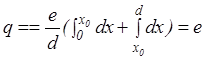                                                      (30)

Первое слагаемое это вклад иона прошедшего путь от х₀ до катода, а второе слагаемое это вклад электрона. В сумме эти так называемые парные частицы дают тот же вклад в протекание заряда во внешней цепи, что и одна частица, родившаяся на катоде и прошедшая до анода.

Функция распределения

При описании характеристик ансамбля частиц вводят так называемую функцию распределения f(r,v,t), которая характеризует плотность числа частиц в фазовом пространстве.

            v

r

По определению f(r,v,t)drdvесть число частиц находящихся в элементарном фазовом объеме drdvвблизи точки (r,v)в момент времени t. Интеграл от функции распределения, взятый по всем возможным скоростям дает плотность или концентрацию частиц в обычном пространстве в момент t.