Заряженные частицы в ЭМ поле. Заряд в потенциальном электрическом поле, страница 3

(31)

Умножая функцию распределения на v, получим плотность потока частиц, имеющих данную скорость, в некоторой точке в некоторый момент времени

, а интегрируя по всем скоростям, получим плотность потока, создаваемого рассматриваемыми частицами в момент времени t в точке r

=    .                       (32)

При умножении на заряд частиц q получаем плотность электрического тока.

Кинетическое уравнение

Чтобы найти функцию распределения, необходимо решить кинетическое уравнение. Изменение функции распределения f(r,v,t) за время dt равно

,                               (33)

где I – интеграл столкновений. Интегралом столкновений называют разность между числом частиц, исчезающих и появляющихся с данной скоростью в окрестности рассматриваемой точки в единице объема в единицу времени в результате столкновений. Учитывая, что

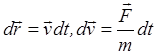,                                                              (34)

где  - сила, действующая на частицу, проведем разложение в ряд. Ограничиваясь линейными членами разложения, получим кинетическое уравнение в следующем виде

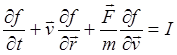                                                                       (35)

Интеграл столкновений

Во многих расчетах для интеграла упругих столкновений используется так называемое t-приближение

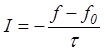                                                                         (38)

где t - некоторое эффективное время между столкновениями, а f₀ – равновесная функция распределения, т.е. считается, что испытав одно эффективное столкновение частицы переходят в равновесное состояние.

Для ионов, находящихся в собственном газе основным является процесс перезарядки, в ходе которого ион превращается в нейтральный атом, а атом превращается в ион. Тогда под tследует понимать характерное время перезарядки, а f₀  можно положить равной n_i(r), где- максвелловская функция распределения по скоростям с температурой газа нейтральных частиц

f_m( =,   

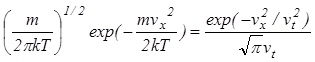Отметим, что отнормирована на одну частицу, т.е. интеграл от нее по скоростям равен 1, а не концентрации.

При наличии неупругих ионизационных процессов учитывая, что скорость образующегося иона практически равна скорости атома, интеграл столкновений, описывающий появление ионов, можно записать в виде

, где G – число генерируемых ионов в единицу времени в единице объема вблизи точки . Полный интеграл столкновений равен сумме интегралов различных столкновительных процессов. Учитывая также, что сила, действующая на ион, это сила Лоренца  можно записать кинетическое уравнение в следующем виде

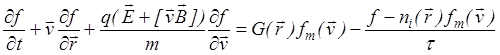
Решение кинетического уравнения представляет собой сложную задачу, осуществляемую, как правило, численными методами. Получение аналитических решений возможно лишь в некоторых частных случаях.

Гидродинамические уравнения

Следует отметить, что во многих случаях достаточное описание ситуации может быть достигнуто при использовании гидродинамических уравнений, которые получают при интегрировании кинетического уравнения. Интегрируя по скоростям получим в стационарном случае так называемое уравнение непрерывности

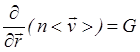
где 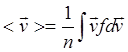 - средняя скорость. Умножая кинетическое уравнение на импульс mvи снова интегрируя по скоростям можно получить после некоторых преобразований уравнение движения.

где 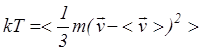, Т – температура. Аналогичные уравнения можно получить для электронов.

Вопросы

1.  Рассчитать скорость двухзарядного иона аргона, прошедшего разность потенциалов 1000 В.

2.  Рассчитать ларморовскую частоту электрона в магнитном поле с индукцией 1 мТл.

3.  Рассчитать ларморовский радиус однозарядного иона гелия в магнитном поле с индукцией 1 мТл. Поперечная скорость иона равна 100 м/с.

4.  Чему равна скорость дрейфа частиц в скрещенных электрическом и магнитном полях Е=1кВ/м, В=10 мТл?

5.  Объясните, почему пара заряженных частиц, образовавшихся в газоразрядном промежутке, дают такой же вклад в ток, что и один электрон, эмиттированный катодом?

6.  Сформулируйте теорему Буша.

Заряд в аксиально - симметричном магнитном поле (теорема Буша)

В этом случае в цилиндрической системе координат (z,r,a) из (1) для изменения угловой составляющей импульса имеем

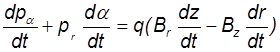                                               (19)

Преобразуем левую часть (19)

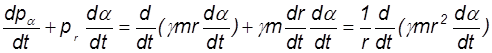.       (20)

Движение в аксиальном и радиальном направлении приводит к изменению магнитного потока Ф, пронизывающего траекторию частицы. Для изменения dФ можно записать

dФ=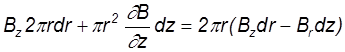                             (21)

Поделив на -dt мы получим в скобках то же выражение, которое стоит в скобках в (19). Воспользовавшись этим обстоятельством и (20) получим

-dФ/dt =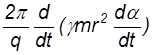                                                  (21)

Интегрируя получаем

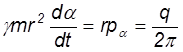(Ф₀-Ф)                                                          (22)

где Ф₀ – магнитный поток при da/dt=0, т.е. момент импульса пропорционален изменению магнитного потока.