Методические указания к лабораторным работам по курсу "Цифровые устройства и микропроцессоры", страница 7

а)                                              б)

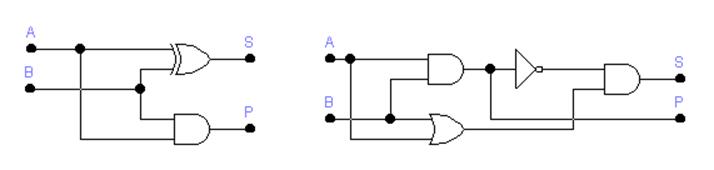
Рис. 2.1 Логические схемы полусумматоров:  (а) – с использованием элемента Исключающего ИЛИ, (б) – на базовых элементах по оптимизированной формуле  (2.4).

Заметим, что схема, синтезированная по формуле (2.3), полученной из таблицы истинности, имеет шесть логических элементов, а вторая схема, оптимизированная с помощью формулы де Моргана (2.4),  всего четыре.

Итак, мы имеем два логических устройства (сумматор по модулю два и полусумматор), которые реализуют арифметическую операцию сложения двух одноразрядных чисел. Сложение многоразрядных чисел сводится к последовательному сложению одноразрядных чисел, при этом, очевидно, что необходимо учитывать не только перенос в следующий разряд, но и перенос от предыдущего разряда. Следовательно,  полный одноразрядный сумматор должен иметь три входа: A, B — слагаемые и P₀ — перенос из младшего разряда и два выхода: сумму Sи перенос в старший разряд P. Повторяя ход рассуждений, которые мы делали при синтезе схемы полусумматора, составим таблицу истинности логической функции, реализующей функции полного одноразрядного сумматора (табл.2.3).

Таблица 2.3         

Мы могли бы далее действовать как обычно, т.е. по таблице истинности полного сумматора записать логические формулы (СДНФ) для суммы и переноса и затем их оптимизировать.  Между тем можно заметить, что для всех четырех нулей переноса P₀ ,; а для всех четырех единичных значений переноса P₀ , . Следовательно, можно сразу записать следующие логические формулы и для суммы S, и для переноса P

,                                         (2.5)

=

= .                                                                               (2.6)

При получении формулы переноса (2.6) мы учли, что дизъюнкцию А+В можно представить как

Формула (2.6) останется верной, если вместо операции Исключающее ИЛИ мы поставим дизъюнкцию. (Почему?). Тогда получится формула переноса в базисе основных логических элементов

Формулы переноса (2.6) и (2.7) состоят из двух функций. Первая функция A*Bназывается функцией генерирования переноса слагаемыми данного разряда, вторая   — функцией распространения переноса из предыдущего разряда.

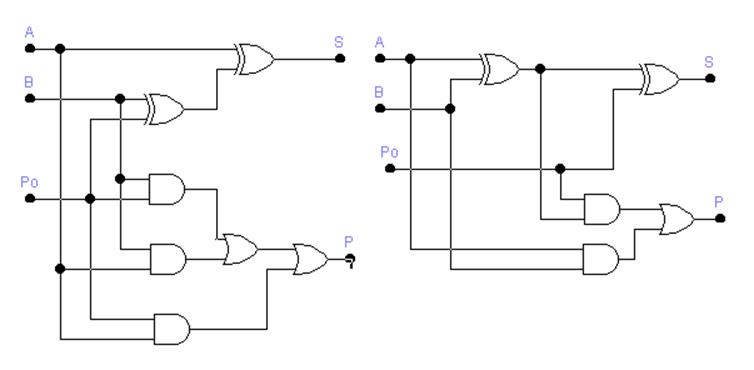
По полученным формулам на рис. 2.2 представлены две логические  схемы полных сумматоров: в одной схеме (а) перенос реализован в базисе основных логических элементов (формула (2.7)); во второй  (б) -  с использованием элемента Исключающее ИЛИ.

а)                                                             б)

Рис. 2.2 Логические схемы полных сумматоров:  с использованием в схеме переноса только основных логических элементов – (а); с использованием в схеме переноса элемента Исключающее ИЛИ – (б).

Все арифметические и логические операции в компьютерах осуществляются в арифметико-логическом устройстве (АЛУ), где комбинационные логические схемы (и прежде всего сумматоры)  выполняют основную работу. Сумматоры изготавливаются на базе интегральных схем (ИС). Для моделирования арифметических сумматоров в программе EWB они представлены в библиотеке Digital двумя базовыми устройствами: полусумматорами и полными сумматорами. Они имеют следующие обозначения на выводах: А, В – входы слагаемых, S — результат суммирования, С₀ – выход переноса, С_i —  вход переноса и используются как самостоятельные комбинационные устройства при построении схем. Многоразрядные арифметические сумматоры строятся из одноразрядных сумматоров. При этом  N —разрядный сумматор, очевидно, будет состоять из одного полусумматора для младшего разряда и (N-1)-го полного сумматора.