Шаг 3. Упростить (оптимизировать) полученную логическую формулу.Упрощать формулы можно несколькими способами. В данном случае упрощения можно сделать, используя основные формулы алгебры логики. Именно надо увидеть, что член A*B*Cсодержит две общие переменные с любым из остальных членов выражения (1.3), затем приписать в выражение (1.3) этот член три раза (в булевой алгебре это можно !), потом вынести за скобки попарно общие члены и, наконец, увидеть, что члены в скобках будут равны 1. В результате получится оптимизированная логическая формула автомата для тайного голосования трех судей по большинству:
![]()
Шаг 4. Построение функциональной схемы по полученной логической формуле. Процедура составления функциональных цифровых схем основана на предположении о том, что логические элементы могут выполнять свои функции в соединениях с себе подобными., Отсюда следует, что можно собирать более сложные цифровые схемы прямо по формуле, представляя аргументы логических функций входами, а операции - базисными логическими элементами. Формула (1.4) записана в дизъюнктивной форме, поэтому схема содержит три элементов И, сигналы с которых поступают на трехвходовый элемент ИЛИ (рис. 1.2). Часто оптимизированная формула с помощью законов Де Моргана переводится в базисы предполагаемой реализации, для которой строится функциональная схема и после выбора конкретных микросхем рисуется принципиальная схема.
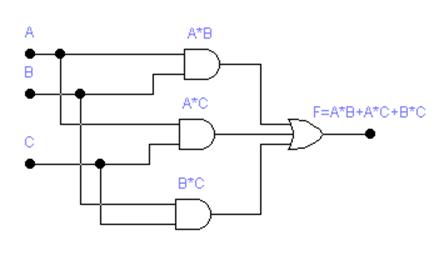
Рис. 1.2. Функциональная схема, составленная по логической формуле (1.4).
5. Порядок выполнения работы
1. Начертить функциональную схему сумматора по модулю два в EWB (Рис.1.1), подключить ее к логическому преобразователю и по таблице истинности убедиться в правильности работы схемы, и с помощью логического преобразователя получить схему сумматора по модулю два в базисе И—НЕ.
2. Начертить функциональную схему голосования по большинству (рис.1.2), подключить ее входы к генератору кодовых слов и к логическому анализатору; выход схемы подключить к отдельной клемме логического анализатора; на генераторе кодовых слов набрать аргументы (входные сигналы) таблицы истинности сумматора: А, В, P0 и, запустив схему, получить на логическом анализаторе осциллограммы таблицы истинности схемы голосования по большинству. Убедиться в правильности работы схемы.
3. Самостоятельно спроектировать схему голосования по большинству трех судей и одного главного судьи. При равном распределении голосов большинство определяется той группой, в которой оказался главный судья. Составить таблицу истинности, записать и оптимизировать с помощью карт Карно ФАЛ. Собрать схему и убедиться в правильности ее работы.
4. Собрать функциональную схему, демонстрирующую работу элемента И в режиме электронного ключа.
5. Самостоятельно спроектировать разрешающую логическую схему, которая бы разрешала прохождение логического сигнала А на выход, только когда управляющие сигналы В и С оба имеют высокий уровень — 1; в противном случае на выходе должен оставаться низкий уровень — 0. Собрать схему и проверить правильность ее работы.
6. Содержание отчета
1.Цели работы.
2.Функциональные схемы с логическим преобразователем, таблица истинности и логические формулы сумматора по модулю два.
3.Функциональная схема с тестовыми приборами (генератор кодовых слов, логический анализатор), ФАЛ, таблица истинности и ее отображение на логическом анализаторе.
4. Функциональная схема, демонстрирующая работу элемента И в качестве электронного ключа.
5. Функциональная схема разрешения по п.4.
6. Краткие выводы по работе.
Контрольные вопросы
1. Выразите логические функции НЕ, И, ИЛИ и ИЛИ—НЕ, через функцию И—НЕ.
2. Определите термины: терм, нормальный терм, конституента нуля, конституента единицы, конъюнкция макстермов, дизъюнкция минтермов.
3. Воспроизведите (на память) все шаги процедуры синтеза функциональной схемы голосования по большинству.
4. Расшифруйте названия двух канонических форм (СДНФ и СКНФ) представления переключательных (логических) функций.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.