Методические указания к лабораторным работам по курсу "Цифровые устройства и микропроцессоры", страница 3

Логические схемы, полученные соединениями логических элементов И, ИЛИ, НЕ, называют комбинационными схемами. Ясно, что каждому способу построения комбинационной схемы из элементарных схем соответствует логическая формула, содержащая только дизъюнкции, конъюнкции и отрицания, и что, обратно, по каждой такой формуле можно построить некоторую вполне определенную комбинационную схему.  Работа комбинационной схемы представляется следующим образом: при подаче на ее входы некоторого набора сигналов через фиксированное время задержки — такт на выходе схемы появляется определенный сигнал – значение логической функции на этом наборе. При этом, если в следующий момент времени на входы будет подан новый набор сигналов, то через такт на выходе схемы появится соответствующий этому набору сигнал, независимо от предыдущего входного сигнала. Независимость реакции от прошлых значений входных сигналов является характеристическим свойством комбинационных схем как устройств без памяти – автоматов из однотактных функциональных элементов.

В общем случае в соединениях, имеющих петли обратных связей, реакция на выходе может зависеть не только от сигналов, поступивших на входы в данном такте, но и от прошлых сигналов. Для описания работы подобных схем необходимо учитывать состояния внутренних элементов схемы, которые «помнят»  реакцию от прошлых сигналов. Зависимость реакции от прошлых значений входных сигналов является характеристическим свойством последовательностных схем как устройств с памятью – конечных автоматов. Изучать элементы памяти и их функционирование мы будем отдельно и позже в работах №4 и №5.

4. Сумматор по модулю два, схема сравнения

 и элементарные функции управления

В табл. 1.1 приведены пять основных операций булевой  алгебры и соответствующие им таблицы истинности. При этом можно забыть о том, что мы рассматриваем какие-то операции над высказываниями, и обратиться  к самим таблицам, как к функциям алгебры логики (ФАЛ), которым можно придавать различный прикладной смысл.

Рассмотрим с этой точки зрения операцию Исключающее  ИЛИ. По записи ее таблицы истинности в столбик (как у нас) легко увидеть, что эта операция правильно складывает двоичные числа только в одном разряде, т.е. перенос в следующий разряд не учитывается.  Таким образом, Исключающее  ИЛИ представляет собой  еще и ФАЛ устройства – двоичного одноразрядного сумматора или сумматора по модулю два. ФАЛ (СДНФ), составленная  по таблице истинности операции исключающего ИЛИ, имеет вид

.                                            (1.1)

Функциональная схема сумматора по модулю два (Исключающего ИЛИ) показана на рис 1.1.

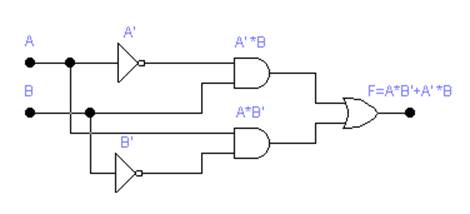
Рис. 1.1. Функциональная схема сумматора по модулю два (Исключающее ИЛИ), построенная на элементах И, ИЛИ, НЕ.

Интересна операция Исключающее  ИЛИ – НЕ, которая  представляет собой инверсию операции  Исключающее  ИЛИ и описывается следующей   ФАЛ 

.                                                  (1.2)

Это двухвходовое устройство, у которого на выходе выдается логическая единица только тогда, когда оба входа имеют один и тот сигнал (0 или 1). Соответствующая схема выполняет функцию сравнения и называется схемой сравнения или равнозначности.

Аналогично рассмотрим ФАЛ операций И, ИЛИ, Исключающее ИЛИ, записав их в одной таблице истинности   табл. 1.2. 

Таблица 1.2.