Методические указания к лабораторным работам по курсу "Цифровые устройства и микропроцессоры", страница 11

Выпускаемые демультиплексоры имеют  2. 4, 8 или 16 выходных каналов. Рассмотрим принцип наращивания размерности выходных каналов на основе использования демультиплексоров меньшей размерности. Принцип наращивания размерности для мультиплексоров был получен из простого преобразования единственной логической формулы. Мы не можем воспользоваться таким способом для мультиплексоров, потому что  у демультиплексора  несколько выходов и соответственно логических функций и их надо реализовать одновременно. Вообще прямой способ одновременной оптимальной реализации логических схем со многими выходами сводится к отысканию общих элементов функций. Однако мы получим принцип наращивания размерности демультиплексоров более экономным и строгим способом – по индукции. Именно, имеем базовый демультиплексор 1-2, реализованный прямым способом. Положим, что построен демультиплексор 1-2^к-1. Тогда демультиплексор 1-2^к можно получить, если к каждому из 2^к-1 информационных выходов уже построенной схемы присоединить информационные входы базовых демультиплексоров 1-2, объявив их выходы выходами схемы демультиплексора 1-2^к. В результате получается каскадная многоярусная схема из демультиплексоров 1-2, в которой первый ярус состоит из одного демультиплексора 1-2, второй – из двух и так далее до к-го яруса. При этом каждый демультиплексор 1-2 имеет адресный вход для выбора одного из двух каналов. По смыслу работы демультиплексоров входной сигнал может поступить на вход только одного из демультиплексоров 1-2 следующего яруса. Поэтому все адресные входы демультиплексоров 1-2 в каждом ярусе можно объединить и объявить адресным  входом выбора одного разряда демультиплексора 1-2^к. Первый ярус состоит из одного демультиплексора 1-2 с единственным адресным входом, который может представлять только один и только старший (к-ый ) разряд номера канала, что следует из общего правила записи чисел в позиционных системах счисления. Второй ярус состоит из двух демультиплексоров 1-2 с соединенными адресными входами, образующие адресный вход выбора (к-1)-го разряда демультиплексора 1- 2^к  —  А_к-1. В зависимости от числа старшего разряда А_k входной сигнал поступит только на один демультиплексоров 1-2 второго яруса и будет переключен на один из двух его выходов в зависимости от значения сигнала А_к-1. Очевидно, что на адресном входе последнего яруса  устанавливается младший разряд номера канала подключения А₀. На рис. 3.6 показана схема DMUX 1-8, составленная из DMUX 1-2.

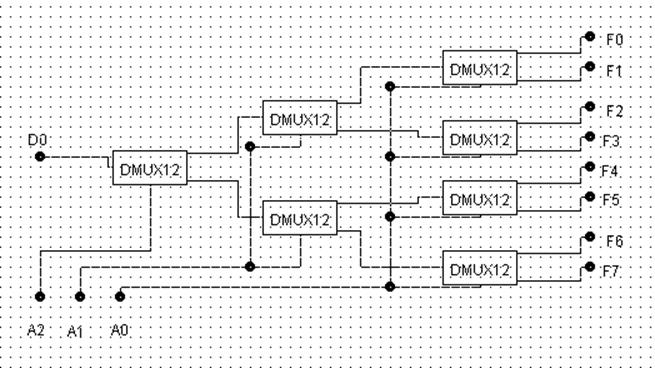
Рис. 3.6.  Демультиплексор 1-8, собранный из демультиплексоров 1-2.

3. Применение мультиплексоров и демультиплексоров

Мультиплексоры и демультиплексоры находят широкое и разнообразное применение в цифровых системах всех видов. Их используют в операциях, связанных с выбором данных, при маршрутизации, установлении последовательности передачи данных, преобразовании параллельных кодов в последовательные, при формировании сигналов и логических функций. Здесь мы рассмотрим принцип использования  мультиплексоров для формирования логических функций на простом примере. Выпишем известную нам логическую формулу (3.2) мультиплексора 4-1

Эта логическая (мультиплексная) функция F характеризуется уникальным свойством: на всех значениях переменных (адресов) А₀, А₁  она равна 1. Но, если в столбце значений функции проставить значения какой-либо другой логической функции, то по принципу работы мультиплексоров они  должны быть проставлены  и в колонке входных данных D. В результате получится реализация заданной таблицей истинности логической функции на мультиплексоре. В этом и заключается принцип реализации логических функций на мультиплексорах. Например, реализуем на мультиплексоре известный нам сумматор по модулю два  по его логической формуле

(3.7)

Это — логическая функция двух переменных, и для ее реализации необходим мультиплексор с двумя адресными входами А₀, А₁ . Запишем формулу сумматора по модулю два в координатах адресов MUX 4-1

.

Таблица истинности заданной функции в координатах MUX 4-1 представлена в табл. 3.3.

Таблица 3.4