Методические указания к лабораторным работам по курсу "Цифровые устройства и микропроцессоры", страница 12

Реализация сумматора по модулю два на MUX 4-1 представлена на рис. 3.4.

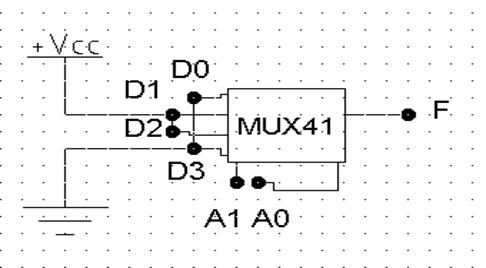
Рис. 3.7. Реализация на MUX 4-1 ФАЛ сумматора по модулю два.

Можно из таблицы истинности MUX N-1 построить любую другую таблицу истинности логической функции от Nпеременных, если на каждый вход данных D₀ , … , D_N подать постоянный сигнал с высоким или низким уровнем, т. е. 0 или 1, в зависимости от данных таблицы истинности логической функции. 

Этот метод реализации логических функций на мультиплексорах во многих случаях более рационален, чем использование дискретных логических элементов. При этом отпадает необходимость в оптимизации логических функций, так как реализация проводится по таблице истинности. Итак, при реализации логических функций на мультиплексорах адресам придается смысл переменных, а входам данных (каналам) –  смысл значений реализуемой логической функции.

Есть еще один, даже более эффективный, метод реализации логических функций. В этом методе используются мультиплексоры, у которых количество адресных входов меньше, чем аргументов у логической функции.  Процедуру этого метода разберем на примере. Пусть необходимо реализовать на MUX 4-1 логическую функцию трех переменных:

                             (3.8)

Для реализации данной функции первым методом необходим MUX 8-1, имеющий три адресных входа, а у MUX 4-1 их два. И еще раз  повторим:   реализация логических функций на мультиплексорах проводится по таблице истинности. У нас таблица истинности MUX 4-1 содержит четыре строки (см. табл. 3.2), а таблица истинности функции (3.4) – 8. Отождествим переменные х₀ и х₁ с входами MUX 4-1 A₀ и А₁ и перепишем исходную функцию F в терминах имеющихся адресных входов, оставив "безадресную" переменную х₂ как есть

(3.9)

Вычислим  таблицу истинности функции F в координатах мультиплексора   4-1  A₀, A₁, принимая "безадресную" переменную х₂ как параметр. После переноса значений функции F входов D (см. табл. 3.2) становится очевидна реализация функции трех переменных (3.8) на MUX 4-1 (рис. 3.8).

Таблица 3.5 

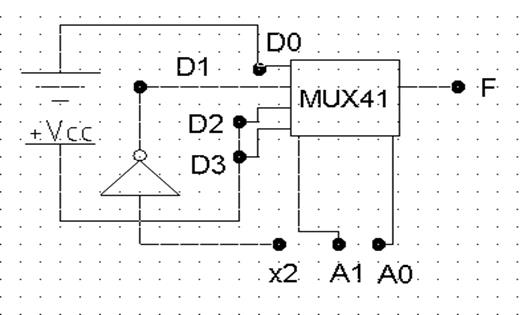
Рис. 3.8. Реализация на MUX 4-1 ФАЛ (3.4) от трех переменных

При использовании мультиплексоров для реализации логических функций на каналы данных подаются сигналы – значения функции, которые они принимают на соответствующих наборах аргументов. Эти сигналы называют настроечными, и, как мы видели, они могут быть константами (0 или 1) и параметрами в виде первичных переменных (см. рис. 3.7 и рис. 3.8). В этих терминах можно сравнить реализации на MUX 8-1 и на MUX 4-1 ФАЛ (3.8) от трех переменных. Реализация вторым методом позволяет уменьшить на единицу число адресных входов мультиплексора и сократить число настроечных входов вдвое. Выбором числа "безадресных" аргументов на любом мультиплексоре второй метод позволяет реализовать логические функции с большим количеством переменных, чем при настройке константами. В то же время настройка константами проще и, поэтому выбор "безадресной" переменной во втором варианте реализации принято считать оптимальным, когда эта переменная реже всех встречается в конъюктивных наборах исходной функции. В этом случае настроечные сигналы содержат максимальное число констант.

4. Порядок выполнения работы

1. Начертить логическую схему MUX  2-1 (см. рис. 3.1),  подключить ее входы к генератору кодовых слов и к логическому анализатору, к которому вдобавок подключить и выход; протестировать работу мультиплексора. Сохранить схему MUX 2-1 как макромодель MUX21. То же самое проделать для логической схемы DMUX 1-2 (рис. 3.6), сохранив ее как макромодель DMUX12.