Методические указания к лабораторным работам по курсу "Цифровые устройства и микропроцессоры", страница 20

В последовательной схеме на управляющем входе каждого триггера устанавливается элемент И, который управляется уровнями разрешения и уровнями (не фронтами) выходного сигнала предыдущего триггера.              На рис. 5.2 показана схема четырехразрядного синхронного двоичного счетчика с последовательной логикой разрешения. В этой схеме переключениями управляют вентили И, а счетные импульсы подаются на триггеры одновременно.   При этом  изменение значений сигналов на выходах всех триггеров будет происходить одновременно и с задержкой, определяемой только одним триггером и всеми элементами логики разрешения.

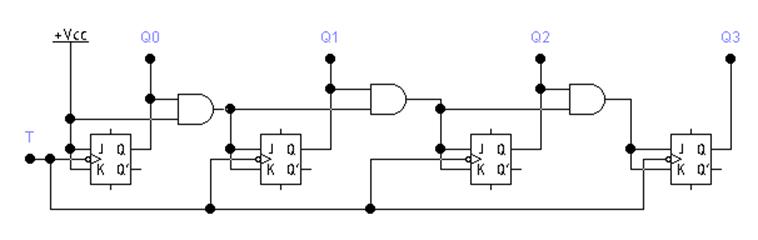
Рис. 5.2. Четырехразрядный синхронный двоичный счетчик с последовательной логикой разрешения

Задержку, даваемую элементами схемы последовательной логики разрешения, можно уменьшить, если для каждого триггера вырабатывать сигнал разрешения вентилем И отдельно и управлять триггерами параллельно. Для этого согласно принципу работы счетчиков на входы разрешающих вентилей каждого триггера достаточно одновременно подать выходные сигналы всех триггеров младших разрядностей. В результате получается  двоичный счетчик с самым высоким быстродействием, который называется параллельный синхронный счетчик или синхронный счетчик с параллельной логикой разрешения (рис. 5.3).

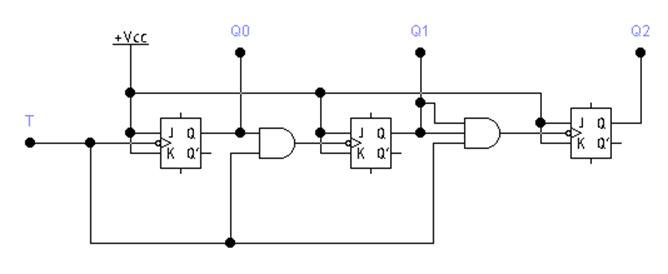
Рис. 5.3. Трехразрядный синхронный двоичный счетчик с параллельной  логикой разрешения.

Но для двоичных счетчиков с параллельной логикой разрешения при увеличении разрядности требуются элементы И с большим числом входов. При этом возникает техническая проблема – выходы триггеров должны обладать высокой нагрузочной способностью, так как  все приборы имеют ограничения на количество подключаемых элементов. Поэтому при проектировании многоразрядных счетчиков с большим количеством разрядов  разряды  разбивают на группы; в каждой группе счетчики строят с параллельной логикой разрешения, а межгрупповые схемы управления реализуют  с помощью последовательной логики разрешения. Обычно в выпускаемых сериях интегральных схем имеется по 5…10 вариантов двоичных счетчиков, выполненных в виде четырехразрядных групп (секций).

3. Двоично-десятичные счётчики

Различные области применения требуют счётчиков с модулями счёта, не кратными 2ⁿ, например, для работы в десятичной системе – M = 10, для схем часов и календарей 60, 24, 7, … и т. д. Но наиболее распространенными счетчиками являются двоично-десятичные. Счетчики с модулем счета          К = 10^m называются двоично-десятичными счетчиками. Двоично-десятичные счетчики чаще всего используются для перевода данных с машинной двоичной системы счисления  в десятичную.

Десятичные цифры одного разряда в двоичной системе представляются четырьмя разрядами. Но четыре двоичных разряда позволяют считать  до 2⁴ = 16. Следовательно, любыми комбинациями десяти из шестнадцати  можно закодировать десятичные цифры. В табл. 5.4 приведены различные способы кодирования десятичных цифр – они называются  D-кодами.

Табл. 5.2