Автоматизированные системы контроля и управления РЭС, конспект лекций, страница 41

Медианой называется средний член вариационного ряда, т. е. ряда, упорядоченного по возрастанию его членов.

Пример: Медиана{0,3,4,0,7}=Медиана{0,0,3,4,7}=3 (рис. 6.7).

Рис. 6.7.

6.11. Алгоритмы цифрового дифференцирования

ЧХ идеального дифференциатора: H(jw)=jw;  j(w)=p/2.

Она может быть аппроксимирована с помощью НФ.

В тех случаях, когда не требуется высокой точности дифференцирования, используется более простые алгоритмы дифференцирования.

а) Двухточечный алгоритм:

y(n)=[x(n)-x(n-1)];  H(z)=(1-z-1);  z₀₁=1.

½H(jw)½=sin (рис. 6.8);  j(w)= - .  Используется в системе СДЦ.

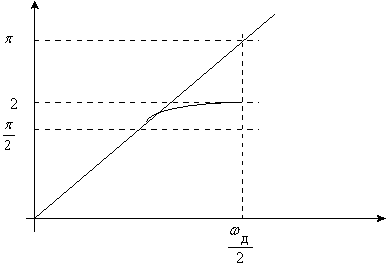
                             Рис. 6.8.

Здесь не подавляются ВЧ - шумы.

б) Трехточечный алгоритм:

y(n)=[x(n)-x(n-2)];  H(z)=(1-z -2);  z₀₁=±1;

½H(jw)½=sin(wT_д).  Здесь имеет место подавление ВЧ - шумов. ЧХ линейна до частот » (рис. 6.9).

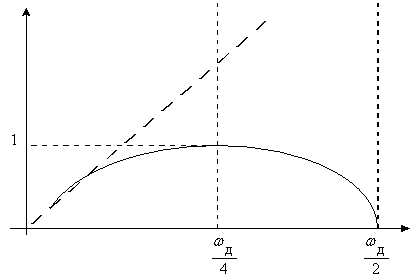
                                                    Рис. 6.9.

6.12. Алгоритмы цифрового интегрирования

ЧХ идеального интегратора: H(jw)=;  j=-.

Цифровые алгоритмы:

а) Алгоритм  прямоугольников:

y(n)=T_дx(n-1)+y(n-1) (рис. 6.10);  z_p1=1;  z₀=0;

½H(jw)½=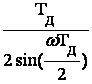 (рис. 6.11);  j(w)=- -.