Автоматизированные системы контроля и управления РЭС, конспект лекций, страница 40

Передаточная функция и ЧХ определяются следующим образом:

H(Z)=;  H(jw)=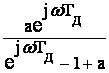;     при w®0, ½H(jw)½®1 (см. рис. 6.6).

Z_p=1-a;  a®0;  Z_p®1 (полюс передаточной функции).

Найдем МО и дисперсию y(n):

M[y(n)]=aM[x(n)]+(1-a)×M[y(n-1)].

В общем случае y(n) является смещенной оценкой x(n).

Если M[y(n)]»M[y(n-1)], то M[y(n)]»M[x(n)] для медленно изменяющихся процессов.

D[y(n)]=a2D[x(n)]+(1-a)2D[y(n)];

Тогда D[y(n)]=.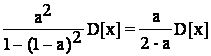

При а=1 D[y]=D[x] - сглаживания нет;

при а®0 D[y]»D[x]®0.

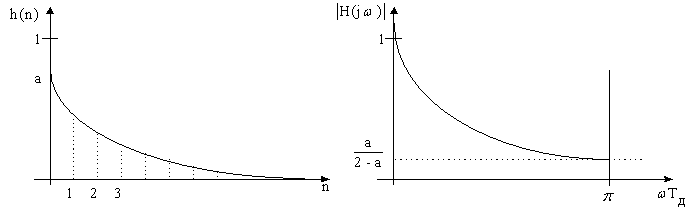
                      Рис. 6.5.                                                                     Рис. 6.6.

Эффективность оценки возрастает с уменьшением а, но при этом сужается полоса пропускания фильтра и снижается чувствительность к изменениям сигнала.

Установка начальных условий:

выполняется по первому измерению: y(-1)=x(0).

Тогда  y(0)=ax(0)+(1-a)x(0)=x(0);

y(1)=ax(1)+(1-a)y(0) и т.д.

Фильтр экспоненциального сглаживания используют также для оценки вариации процесса:

g(n)=(n)/B(n), где (n)=a(n)+(1-a)(n-1) - среднее (сглаженное) значение ошибки; e(n)=y(n)-x(n) - ошибка сглаживания;

B(n)=a½e(n)½+(1-a)B(n-1)    - сглаженное значение модуля ошибки ½e(n)½.  Является оценкой СКО: B»0.8s_e. Коэффициент а выбирается, как правило, эмпирически.

6.10. Алгоритм нелинейной медианой фильтрации

Обеспечивает хорошую передачу быстрых изменений (перепадов) сигнала, которые сглаживаются линейными фильтрами. Определение медианного фильтра:

y(n)=Медиана {x(n-),…x(n),…x(n+)}, L - нечетное.