Автоматизированные системы контроля и управления РЭС, конспект лекций, страница 39

D[₀(n)]=LD[x(n+k)]= - в L раз меньше дисперсии исходных данных.

D[₁(n)]=.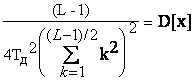

6.8. Рекурсивная реализация алгоритма скользящего среднего

Цель - уменьшить объем вычислений.

L₀(n)=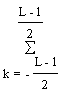x(n+k); L₀(n-1)=.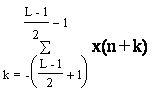

Тогда  L₀(n)=L₀(n-1)+[x(n+) - x(n-)].

₀(n)=₀(n-1)+[x(n+) - x(n-)].

6.9. Алгоритм квазиоптимальной динамической фильтрации

с помощью РФ 1-го порядка (по бесконечному набору данных)

Недостаток НФ - это необходимость помнить и использовать при вычислениях на каждом шаге весь текущий набор данных. Этот недостаток отсутствует в РФ, но получаемые при этом оценки могут быть не оптимальными.

Алгоритм экспоненциального сглаживания (фильтрации).

y(n)=a×x(n)+(1-a)×y(n-1)=x(n)+y(n-1);

a==(0…1), где М - коэффициент сглаживания. Чем больше М, тем сильнее эффект сглаживания.

Найдем ИХ фильтра:

n=0; h(0)=a; n=1; h(1)=a(1-a); n=2; h(2)=a(1-a)2;

   (рис. 6.5).