Автоматизированные системы контроля и управления РЭС, конспект лекций, страница 38

где ₀(n), ₁(n) - коэффициенты сглаживающей функции, получаемые по экспериментальным данным. Они имеют смысл среднего сглаженного значения данных при k=0: ₀(n)=(n+k)½_k=0 и сглаженного значения скорости ₁(n) изменения данных на интервале LT_д, также отнесенной к моменту времени nT_д  (рис. 6.4).

Рис. 6.4.

Оценки ₀(n) и ₁(n) получаются с помощью МНК:

e­­­­(S₀,S₁)=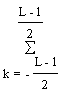{x(n+k)-[S₀(n)+S₁(n)×k]}2 - сумма квадратов ошибок.

Далее находят частные производные: =0; =0.

Решают систему из двух уравнений и находят выражения для ₀(n) и ₁(n):

₀(n)=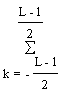x(n+k). Этот алгоритм известен как скользящего среднего.

₁(n) = 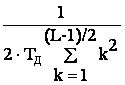×[x(n+k)-x(n-k)] - оценка скорости (м/c) или алгоритм многоточечного (L-точечного) дифференцирования.

При сглаживании полиномом 2-го порядка можно найти также оценку ускорения ₂(n) (параболическая траектория). При этом L=5, 7, 9, 11 (не более). Как видим, этот алгоритм реализуется с помощью нерекурсивных фильтров (НФ).

Дисперсия оценок: