Ядерная физика: Учебно-методическое пособие для проведения практических занятий, страница 9

19.  Протоны, налетающие на неподвижную литиевую мишень, возбуждают реакцию ⁷Li(p,n)⁷Be. При какой кинетической энергии протона  возникший нейтрон может оказаться покоящимся.

Тема 4

Сечение реакции. Упругое рассеяние нейтронов

Обозначим символом f совокупность параметров, идентифицирующих продукты реакции: тип образовавшейся частицы, ее масса, а также квантовые числа, описывающие ее полный момент импульса, спин, внутренняя четность и другие внутренние характеристики частицы, если от них зависит вероятность ее возникновения в ходе реакции. В этом случае будем говорить, что реакция протекает по каналу f, либо реакция имеет выход f.  Тип образующихся частиц зависит от энергии налетающей частицы и, возможно, некоторых других ее характеристик (например, спина при достаточно высоких энергиях). При энергиях выше пороговых значений возможны эндоэнергетические реакции, которые не идут при более низких энергиях. В отличие от макроскопических явлений, реакции упругого рассеяния происходят всегда. Поэтому всегда говорят о наличии упругого канала реакции.

Будем считать, что число частиц dn_f с параметрами, входящими в совокупность f, образующихся в единицу времени в результате реакции и имеющих импульсы в интервале от  до , пропорционально плотности потока j налетающих на мишень частиц и числу частиц N_f мишени, на которых могут происходить реакции с выходом f. Коэффициент пропорциональности называется элементарным микроскопическим сечением ds_f  реакции по каналу fи вычисляется по формуле (4.1),

. (4.1)

Интегрирование (4.1) по всем величинам импульсов  и их направлениям дает полное сечение s_f  реакции по каналу f. В качестве элемента интегрирования здесь естественно взять элементарный объем d³p_f  импульсного пространства, образуемого концами всех возможных векторов , лежащих в интервале от  до . Этот элемент объема можно представить в виде

 ,

где dW - элемент телесного угла, в котором лежат векторы импульса в интервале от  до ;

 dp_f - интервал изменения их величины.

Тогда имеет смысл рассматривать величину элементарного микроскопического сечения реакции, отнесенную к единице телесного угла, - так называемое элементарное дифференциальное микроскопическое сечение реакции по каналу f:

. (4.2)

Относя дифференциальное микроскопическое сечение реакции по каналу f  к интервалу изменения величины импульса dp_f частиц вида f, образующихся в результате реакции, получим величину, которую можно назвать распределением дифференциального микроскопического сечения по импульсам образовавшихся частиц. Однако чаще более удобно говорить о распределении не по величинам импульсов образовавшихся частиц, а их энергий E_f – энергетическом распределении (энергетической плотности) дифференциального микроскопического сечения:

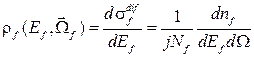, (4.3)

где  - единичный вектор, указывающий направление движения продуктов реакции сорта f.

Интегрирование  по всем возможным значениям энергии E_f  и направлениям  дает полное микроскопическое сечение реакции по каналу f:

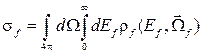.      (4.4)

В задачах, в которых на тонкую мишень налетает узкий пучок частиц, можно воспользоваться законом ослабления узкого пучка:

, (4.5)

где j₀ – первоначальное значение плотности потока налетающих частиц;

 x - глубина мишени, на которую проник пучок;

 k – линейный коэффициент ослабления, который определяется как сумма произведений полных микроскопических сечений реакций по всевозможным каналам f, допустимых при заданной энергии налетающих частиц, на число частиц мишени в единице объема n_0f, на которых могут происходить реакции по каналу f:

. (4.6)

Произведение

 (4.7)

называется макроскопическим сечением реакции  по каналу f. Поэтому линейный коэффициент ослабления имеет смысл полного макроскопического сечения реакций взаимодействия налетающих частиц с частицами мишени.

В случае гетерогенных мишеней вероятность Pr_f протекания реакции по каналу f определится как отношение макроскопического сечения реакции по каналу f к полному макроскопическому сечению: