Ядерная физика: Учебно-методическое пособие для проведения практических занятий, страница 6

15.  Получить с помощью полуэмпирической формулы для энергий связи выражение, определяющее разность энергий связи двух зеркальных ядер с нечетным массовым числом A. Вычислить разность энергий связи следующих зеркальных ядер: а)  и ; б)  и .

16.  Разность энергий связи зеркальных ядер  и   МэВ. Вычислить радиусы этих ядер, считая, что  обусловлена различием только энергии электростатического отталкивания протонов, которая равна  (− радиус ядра).

Тема 3

Кинематика ядерных реакций
в нерелятивистском приближении. Учет энергии реакции

Словосочетание «кинематика ядерных реакций» охватывает совокупность задач о нахождении импульсов и энергий частиц из законов сохранения без рассмотрения законов взаимодействия частиц. Физические особенности взаимодействия определяют один из свободных параметров в  системе уравнений, описывающей законы сохранения импульса и энергии. В задаче, описываемой уравнением реакции , закон сохранения импульса (1.1) и закон сохранения энергии (1.3) составляют систему из трех уравнений с четырьмя неизвестными, в качестве которых выступают импульсы образовавшихся частиц, описываемые проекциями на оси декартовой системы координат, вводимой в плоскости движения частиц.

Рассмотрим эту задачу в общем виде в нерелятивистском приближении. Ограничимся здесь случаем, когда ядро A в лабораторной системе отсчета (л-системе) покоится. Пусть  - кинетическая энергия налетающей частицы а (для упрощения дальнейшей записи индекс а у кинетической энергии опускаем). 

В системе отсчета, связанной с центром инерции, (с-системе) суммарный импульс частиц до реакции равен нулю. Тогда в силу закона сохранения импульса (1.1) суммарный импульс частиц, образовавшихся в результате реакции, также равен нулю:

 (3.1)

Здесь все величины, отнесенные к с-системе, снабжены индексом с. Если  - единичный вектор вдоль направления движения налетающей частицы a в с-системе, а  - единичный вектор вдоль направления движения образовавшейся частицы b в с-системе, то из (3.1) следует, что

    (3.2)

Угол между векторами  и  обозначается χ: . Его величина определяется законом взаимодействия частиц, вступающих в реакцию и возникающих в результате нее, и обычно выбирается в качестве свободного параметра теории.

Из (3.2) следует, что в с-системе закон сохранения энергии (1.3) в нерелятивистском приближении

 (3.3)

упростится к виду

 (3.4)

    ,     (3.5)

где m, m’ – приведенные массы частиц, вступающих в реакцию, и частиц, образовавшихся в результате реакции.

Из (3.4) можно найти величину импульса частиц, образовавшихся в результате реакции:

. (3.6)

В л-системе . Поэтому полный импульс частиц, вступающих в реакцию, равен импульсу налетающей частицы . Следовательно, скорость движения центра инерции

. (3.7)

Зная ее, можно найти скорости частиц в с-системе с помощью закона сложения скоростей Галилея, а по ним вычислить соответствующие импульсы. Так, импульс налетающей частицы в с-системе

, (3.8)

откуда видно, что вектор  в системе центра инерции имеет то же направление, что и импульс налетающей частицы в л-системе, который можно представить в виде . Из уравнений (3.2), (3.6), (3.8) и связи импульса налетающей частицы в л-системе с его кинетической энергией  в этой же системе отсчета получим, что величина импульса  образовавшихся частиц в с­-системе связана с энергией налетающей частицы в л-системе выражением

, (3.9)

где

.         (3.10)

Из (3.9) и (3.10) видно, что при Q < 0 величина E ограничена снизу условием , где Е_пор определяется по формуле (1.4). 

Зная величину импульса p_c’(3.9) и закон сложения скоростей, с учетом второго определения (3.2) и выражения (3.7) можно найти импульсы и энергии частиц, образовавшихся в результате реакции:

, (3.11)

 , (3.12)

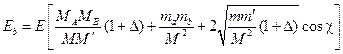, (3.13)

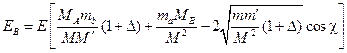, (3.14)

где , .

Углы разлета образовавшихся частиц в л-системе вычисляются из выражений (3.11) и (3.12) по следующим формулам: