Физика \ Ядерная физика

Ядерная физика: Учебно-методическое пособие для проведения практических занятий, страница 16

Радиоактивные семейства.
Переменное равновесие. Вековое равновесие

Часто дочерний элемент радионуклида сам оказывается радиоактивным. В результате образуются цепочки радиоактивных превращений, а совокупность материнского и дочерних радионуклидов называется радиоактивным семейством. Ядро конечного элемента семейства является стабильным, и этот элемент также включается в семейство.

Простейшее радиоактивное семейство, состоящее из материнского и одного дочернего радионуклида, превращающегося в стабильный элемент, описывается следующей системой дифференциальных уравнений:

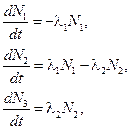  (7.1)

где l1 - постоянная распада материнского нуклида; l2 - постоянная распада дочернего нуклида.

Система (7.1) должна быть дополнена начальными условиями: в момент времени t = 0 начала наблюдения за цепочкой распадов в образце был только первый радионуклид:

  (7.2)

Решение системы (7.1) при начальных условиях (7.2) имеет следующий вид:

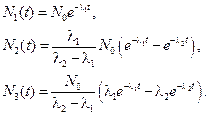  (7.3)

При l2 > l1 отношение

  (7.4)

со временем стремится к постоянному значению

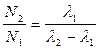.  (7.5)

Этот случай называется состоянием переменного (радиоактивного) равновесия.

Вековое равновесие

                                            (7.6)

имеет место при , или l2 >> l1, и показывает, что число распадов дочерних ядер равно числу распадов материнских ядер (т. е. числу образовывающихся дочерних ядер).

Примеры

7.1. Радиоизотоп X1 с постоянной распада превращается в радиоизотоп X2 с постоянной распада  по цепочке:  (стабилен). Считая, что в начальный момент времени препарат содержал только ядра изотопа X1, в количестве , найти законы изменения числа ядер изотопов X1, X2 и X3 со временем.

Дано

Решение

X1:

X2:

X3 стабилен

:

_____________

Радиоизотоп X1 распадается по цепочке

 (стабилен).                          (1)

Изменение числа  ядер X1, числа  ядер X2 и числа  ядер X3 в единицу времени определяется уравнениями

                                                              (2)

             ,                                            (3)

             .                                                   (4)

Эти уравнения имеют следующий смысл:

–  количество ядер X1 убывает за счет их распада;

–  количество ядер X2 убывает за счет их собственного распада и пополняется за счет распада ядер X1;

–  количество ядер X3 накапливается за счет распада ядер X2.

Если в начальный момент времени  имеется  ядер X1, а ядер X2 и X3 нет, т. е.

             , , ,                               (5)

то при начальных условиях (5) решения дифференциальных уравнений (2), (3) и (4) имеют вид

                                                       (6)

                                             (7)

                                    (8)

Ответ:     ,

7.2. Радиоизотоп X1 испытывает превращения по цепочке (над стрелками указаны соответствующие постоянные распада). Считая, что в начальный момент времени препарат содержал только ядра изотопа X1 в количестве , найти законы изменения числа ядер изотопов X1, X2 и X3 со временем.

Дано

Решение

X1:

X2:

X3:

:

_________

Радиоизотоп X1 испытывает превращения по цепочке

            

Изменение числа  ядер X1, числа  ядер X2 и числа  ядер X3  в единицу времени определяется уравнениями

                                                       (1)

        ,                                      (2)

.                                     (3)

Эти уравнения имеют следующий смысл:

–  количество ядер X1 убывает за счет их распада;

–  количество ядер X2 убывает за счет их собственного распада и пополняется за счет распада ядер X1;

–  количество ядер X3 убывает за счет их собственного распада и пополняется за счет распада ядер X2.

Если в начальный момент времени  имеется  ядер X1, а ядер X2 и X3 нет, т. е.

             , , ,                            (4)

то при начальных условиях (4) решения дифференциальных уравнений (1),(2) и (3) имеют вид

                                                                (5)

,                                              (6)

.   (7)

Ответ:      ,

.
Скачать файл