Ядерная физика: Учебно-методическое пособие для проведения практических занятий, страница 4

5.  Определить с помощью табличных значений масс нуклидов энергию следующих реакций:      а) ⁷Li(p,n)⁷Be;       б) ⁷Li(a,n)¹⁰Be;       в) ⁹Be(n,g)¹⁰B;       г) ¹⁶O(d,a)¹⁴N.

6.  Определить энергию, выделяющуюся в акте синтеза дейтерия: .

7.  Определить энергии следующих реакций:           а) ³H(p,g)⁴He;
б) ¹⁴N(a,d)¹⁶O;   в) ¹²C(a,d)¹⁴N;                  г) ⁶Li(d,na)³He.

8.  Известны удельные энергии связи ε,  ε₁ , ε₂  ядер, участвующих в реакции деления . Определить энергию , выделяющуюся в процессе деления.

9.  Считая, что в одном акте деления ядра  освобождается энергия 200 МэВ, определить массу изотопа , подвергшегося делению при взрыве атомной бомбы с тротиловым эквивалентом 30 кт, если тепловой эквивалент тротила равен 4,1 кДж/г.

10.  Вычислить с помощью таблиц массу атома , если известно, что энергия реакции ¹⁷O(n,p)¹⁷N           МэВ.

11.  Вычислить пороговые энергии α-частиц и нейтронов в следующих реакциях:

12.  Вычислить пороговую кинетическую энергию  налетающей частицы в реакции , если налетающей частицей является: а) протон; б) ядро трития .

13.  При облучении моноэнергетическим пучком протонов мишеней из лития и бериллия было обнаружено, что реакция ⁷Li(p,n)⁷Be (энергия реакции  МэВ) идет, а реакция ⁹Be(p,n)⁹B (энергия реакции  МэВ) не идет. Найти возможные значения кинетической энергии  протонов.

14.  Найти пороговую кинетическую энергию α-частицы для возбуждения реакции ⁷Li(a,n)¹⁰B. Какова при этом скорость ядра ?

15.  Протон с кинетической энергией  МэВ захватывается покоившимся ядром ²H. Найти энергию возбуждения образовавшегося ядра.

Тема 2

Энергия связи ядер

Энергией связи ядра называется минимальная энергия, которую надо сообщить ядру, чтобы разделить его на нуклоны:

,                  (2.1)

где m_p, m_n, M(Z,A) ­– массы протона, нейтрона и соответствующего атомного ядра.

Удельной энергией связи называется энергия связи, отнесенная к массовому числу:

e_св = Е_св / А                                             (2.2)

Энергия отделения нуклона (энергия связи нуклона в ядре) - это минимальная энергия, которую нужно сообщить ядру, чтобы отделить от него нуклон. Энергия связи нейтрона в ядре

    или

,                             (2.3)

а энергия связи протона в ядре

     или

.                            (2.4)

Можно также говорить об энергии связи любой части ядра относительно другой. Например, энергия связи a-частицы в ядре может быть рассчитана по формуле (2.5).

,         или

.          (2.5)

Если происходит процесс слияния ядра с нуклоном или другой частицей, то выделяется энергия, называемая энергией присоединения.

Полуэмпирическая формула (формула Вайцзекера) для энергии связи ядра:

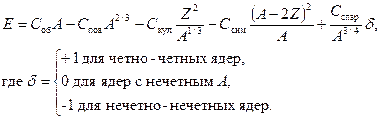         (2.6)

Слагаемые в формуле (2.6) соответствуют модельным представлениям о строении атомного ядра и учитывают, соответственно, объемную, поверхностную, кулоновскую энергии, энергию симметрии и энергию спаривания. Коэффициенты в формуле (2.6) названы соответственно и подбираются так, чтобы наблюдалось наилучшее согласие с опытом:

Примеры

2.1. Найти энергию связи, приходящуюся на один нуклон ε, в ядрах .