Статистические методы обработки данных в экологии: Методические рекомендации по изучению дисциплины, страница 8

Сравнение средних необходимо проводить в следующем порядке. Сначала сравнить группу с наибольшим выборочным средним с группой имеющей наименьшее выборочное среднее, затем с группой с наименьшим выборочным средним среди остальных групп и т.д. Когда при сравнении обнаружится, что μ_j и μ_t различаются незначимо или не останется группы с меньшим выборочным средним, следует заменить группу с наибольшим средним на группу со вторым по величине средним и начать процедуру сначала.

Однофакторный дисперсионный анализ в модели со случайными эффектами

В модели со случайными эффектами совокупности, соответствующие различным уровням фактора, выбираются случайно из большого (бесконечного) числа совокупностей. Каждой совокупности присваиваются номер от 1 до k и j-я совокупность считается соответствующей j-му уровню фактора. Из каждой совокупности случайно выбираются n объектов и рассматриваются значения x_1j, x_2j, ..., x_nj. Предполагается, что эти наблюдения распределены нормально со средним m_j и дисперсией σ², не зависящей от уровня j фактора. Кроме того, предполагается, что средние
m₁, ..., m_k представляют собой случайную выборку из совокупности, распределенной нормально со средним μ и дисперсией σ_a².

Модель однофакторного дисперсного анализа со случайными эффектами описывается уравнением

,

где a_j – дифференциальный эффект уровня фактора, который представляет собой случайную величину, распределенную нормально с нулевым средним и дисперсией σ_a².

В этой модели нас тоже интересует, есть ли изменчивость между группами, однако интерпретация такой изменчивости иная. Теперь проверяется гипотеза H₀: σ_a² = 0 при H₁: σ_a² ≠ 0, означающая, что фактор не вносит никакого вклада в дисперсию. Можно показать, что проверкой этой гипотезы используется то же самое F-отношение:

.

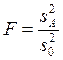Подчеркнем, что в реальной задаче выбор модели дисперсионного анализа производится фактически при принятии решения о целях исследования и способе взятия выборки.

Проверка однородности дисперсий

При использовании стандартных методов дисперсионного анализа необходимо условие равенства дисперсий остаточных случайных величин. Если нет уверенности в том, что это условие выполняется, следует проводить проверку однородности дисперсий.

Чтобы избавиться от серьезных сомнений в применимости стандартного метода, должно быть веское подтверждение однородности дисперсий, поэтому при проверке часто используется очень малый уровень значимости (порядка 0.001). При больших объемах выборок могут использоваться большие уровни.

В критерии Барлетта для проверки гипотезы H₀: σ₁² =...= σ_k² используется статистика

,

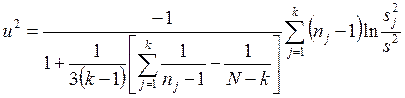где  – оценка дисперсии j-й совокупности и  – объединенная оценка дисперсии, которые определяются из выражения:

, ;

, .

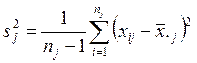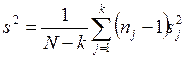Эта статистика имеет распределение χ² с k-1 степенями свободы.

Критерий Кочрена основан на статистике

,

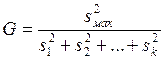при этом объемы выборок, по которым рассчитаны  одинаковы.

Распределение этой статистики известно точно и зависит от числа степеней свободы n-1 и количества выборок. Критические значения статистики G находят по таблицам процентных точек распределения Кочрена.

Двухфакторный дисперсионный анализ с пересечением уровней факторов

В двухфакторном дисперсионном анализе изучается влияние на исследуемую величину двух факторов A и B, каждый из которых имеет конечное число уровней. При этом ставится задача о том, как влияют и влияют ли вообще эти факторы на исследуемую величину.

Два фактора A и B называются пересекающимися, если в плане эксперимента предусмотрены все возможные сочетания факторов. Поэтому для фактора A с k уровнями и фактора B с n уровнями такой план должен содержать по меньшей мере одно наблюдение для каждой из kn комбинаций уровней. Комбинацию ij, где i– уровень фактора А, а j– уровень фактора В, называют ij-ячейкой. В каждой ячейке располагаются значения случайной величины X, полученной при m повторных наблюдениях. Результаты наблюдений можно представить в виде таблицы