Статистические методы обработки данных в экологии: Методические рекомендации по изучению дисциплины, страница 10

5.2 Основные теоретические сведения

Ранговый однофакторный анализ

Если ничего не известно о распределении наблюдений, полученных при различных уровнях фактора, то для проверки совпадения нескольких средних часто используют информацию, которая содержится в рангах наблюдений x_ij при их упорядочении в порядке возрастания. Обозначив через r_ij ранг значения x_ij, получим следующую таблицу.

В рамках ранговых критериев нулевая гипотеза формулируется как гипотеза H₀: все k совокупностей (столбцов таблицы) одинаково распределены. Строго говоря, если нулевая гипотеза отвергается, то можно только утверждать, что распределения совокупностей различны. Это, однако, не означает, что их средние не равны между собой. Для вывода о том, что выборки производились из совокупностей с различными средними, необходимо предположить, что эти совокупности одинаковы по всем другим параметрам. На практике, однако, допустимы умеренные отклонения от этого правила.

Непараметрический критерий Краскела-Уоллиса для проверки нулевой гипотезы основан на статистике

,

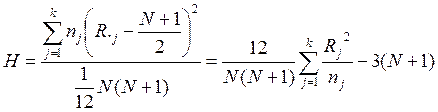где 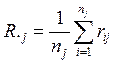– средний ранг, рассчитанный по j-му столбцу; 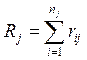 – сумма рангов j-го столбца; 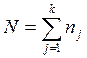 – общее число наблюдений.

Для небольших объемов выборок имеются таблицы процентных точек распределения статистики Краскела-Уоллиса. При больших объемах выборок статистика H при справедливости нулевой гипотезы распределена приближенно по закону χ² с k-1 степенями свободы. Если в таблице данных есть совпадающие значения, то при их ранжировании следует использовать средние ранги. Если совпадений много, то рекомендуется применять модифицированную форму статистики H:

,

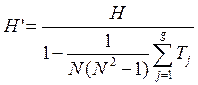где g – число групп совпадающих наблюдений; ;  – число совпадающих наблюдений в группе с номером j.

Ранговый двухфакторный анализ

Рассмотрим двухфакторный эксперимент, когда на уровнях фактора В проведено по одному наблюдению (неповторяемый эксперимент), при котором таблица данных имеет следующий вид

В отличие от факторного анализа ранжирование осуществляется не по всей совокупности величин x_ij, а по строкам (для проверки однородности данных по столбцам таблицы данных), т. е. ранжируется каждая отдельная строка таблицы данных. Этим устраняется влияние "мешающего" фактора В, значение которого для каждой строки постоянно.

Для проверки гипотезы H₀: влияние фактора A (эффектов столбцов) отсутствует, при H₁: влияние фактора A есть, используется статистика Фридмана

,

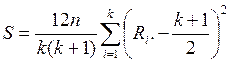где 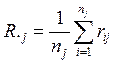– средний ранг, рассчитанный по j-му столбцу;     r_ij – ранг величины x_ij.

При вычислениях удобно использовать другую запись статистики:
                     .

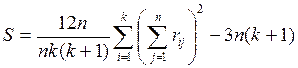Для небольших значений k и n имеются таблицы процентных точек распределения статистики Фридмана, позволяющие при заданном уровне значимости  находить критические значения S(k, n, ). Гипотеза H₀ не отвергается, если расчетное значение статистики меньше критического.

При больших n при справедливости нулевой гипотезы статистика S аппроксимируется распределением χ² с k-1 степенями свободы.

Если в строках таблицы данных имеются совпадающие значения, при переходе к таблице рангов используются средние ранги, а вместо статистики S используется ее модификация.

Для проверки гипотезы об эффектах фактора В (строк) следует поменять местами строки и столбцы таблицы данных.

5.3 Вопросы для самоконтроля