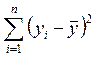Статистические методы обработки данных в экологии: Методические рекомендации по изучению дисциплины, страница 14

 – сумма квадратов отклонений наблюдений относительно среднего значения наблюдений, ее называют полной (общей суммой) квадратов СК_П.

 – сумма квадратов отклонений значений линии регрессии относительно среднего наблюдений, ее называют суммой квадратов обусловленной регрессией, СК_р.

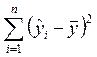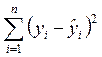 – сумма квадратов отклонений наблюдений относительно значений линии регрессии, ее называют остаточной суммой квадратов СК₀.

Подчеркнем, что приведенное тождество справедливо только при наличии в модели параметра a.

Вычисления по проверке значимости регрессии проводят в следующей таблице дисперсионного анализа

Если ошибки ε_i распределены по нормальному закону, то при справедливости H₀: b = 0 статистика 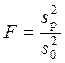 распределена по закону Фишера с числом степеней свободы 1 и n-2. Нулевая гипотеза будет отклонена на уровне значимости α, если значение статистики F будет больше α-процентной точки распределения Фишера.

При условии, что ошибки ε_i имеют нормальное распределение, оценки  и , являющиеся линейными комбинациями нормально распределенных величин, тоже распределены нормально с параметрами

Поскольку истинное значение дисперсии σ² неизвестно, его заменяют оценкой s₀². Это позволяет обычными методами построить доверительные интервалы для параметров a и b.

Проверка адекватности модели регрессии

Проверка адекватности модели простой линейной регрессии (под адекватностью понимается, что никакая другая модель не дает значимого улучшения в предсказании отклика) может быть осуществлена в случае, если наблюдения отклика проводились при одинаковых значениях переменной X два или более раз. Тогда модель регрессии будет иметь вид

,      ;     .

Оценки параметров даются иногда выражениями:

,

,

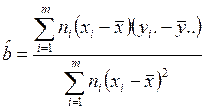где

;         ;       .

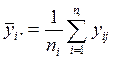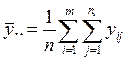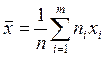Можно показать, что при наличии повторных наблюдений отклика остаточную сумму квадратов СК₀ можно представить в виде

.

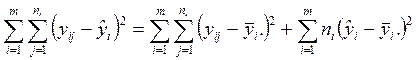Первый член в правой части – это сумма квадратов “чистых” ошибок, второй член – сумма квадратов неадекватности. Последняя сумма имеет m-2 степеней свободы, следовательно, дисперсия неадекватности

.

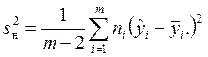Статистикой критерия для проверки гипотезы H₀: простая линейная модель адекватна, против гипотезы H₁: простая линейная модель неадекватна, является случайная величина

.

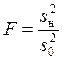При справедливости нулевой гипотезы статистика F имеет распределение Фишера со степенями свободы m-2 и n-m. Гипотеза линейности линии регрессии должна быть отвергнута на уровне значимости α, если полученное значение статистики больше α-процентной точки распределения Фишера с числом степеней свободы m-2 и n-m.

Отметим сходство между суммой квадратов “чистых” ошибок и внутригрупповой суммы квадратов в однофакторном дисперсионном анализе.

Коэффициент детерминации

Иногда для характеристики качества линии регрессии используют выборочный коэффициент детерминации , который показывает, какую часть сумма квадратов, обусловленная регрессией СК_р, составляет в полной сумме квадратов СК_п:

,

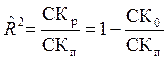где СК₀ – остаточная сумма квадратов.

Чем ближе  к единице, тем лучше регрессия аппроксимирует экспериментальные данные, тем теснее наблюдения примыкают к линии регрессии.

Вместо коэффициента детерминации  в прошлом использовалась статистика, которой некоторые исследователи отдавали предпочтение. Это так называемая нормированная (приведенная) R² статистика

,

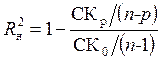где p – число параметров линейной модели регрессии.

Применительно к простой линейной регрессии

.

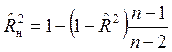В случае простой линейной регрессии коэффициент R² равен квадрату коэффициента корреляции r².

7.3 Вопросы для самоконтроля

1.  Какие задачи решаются в регрессионном анализе?